一个问题可以通过不同的角度来进行观察和求解，那么对于优化问题，它的对应的角度是什么呢？是对偶问题
…

涉及到的知识点

• Lower bound property
• Strong and Weak Duality
• Complementary Slackness
• KKT Conditions

对于KKT Conditions，把它放到了SVM中去讲解，本文不再赘述。

Primal Problem & Dual Problem

原始问题（Primal Problem）和对偶问题（Dual Problem）是对一个问题的不同角度上的理解，任何一个原始问题都可以转换为与之对应的对偶问题。

举个例子，就像初中时学过的三视图一样，你从正面观察得到的正视图是一个样子，从侧面观察的左视图和从上面观察的俯视图是另外一个样子。根据这些不同的视图就可以唯一确定出来这个物体的立体形状。

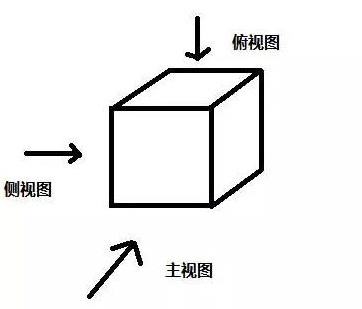
原始问题就相当于是从正面、左侧面和上面俯视得到的三视图；而对偶问题就相当于从背面、下面和右侧面观察得到的三视图，它们是同一问题的从不同方面的表述。

根据上述的举例，可以直观的感觉出来：任何一个原始问题从原则上来讲，都可以将其转换为与之对应的对偶问题，然后求解这个对偶问题得出来的解经过一些调整来得到原始问题的解。上述表述在凸优化中就对应着拉格朗日对偶问题。

拉格朗日对偶问题

一般优化问题的标准形式转为对偶问题

将给定一般优化问题的标准形式：

$$\begin{aligned} \min \quad &f_0(x) \\ s.t. \quad &g_i(x) &\le 0, &i = \{1, 2, 3, ..., m\} \\ &h_j(x) &=0, &j = \{1, 2, 3, ..., n\} \end{aligned}$$

转为拉格朗日函数的形式：

$$L(x, \lambda, \nu) = f_0(x) + \lambda\sum^{m}_{i = 1}g_i(x) + \nu\sum^{n}_{j = 1}h_j(x)\quad (\lambda \ge 0, \nu \ge 0)$$

最后将拉格朗日函数的形式转为对应的拉格朗日对偶函数：

$$\begin{aligned} g(\lambda, \nu) &= \inf_xL(x, \lambda, \nu) \\ &=\inf_x[f_0(x) + \lambda\sum^{m}_{i = 1}g_i(x) + \nu\sum^{n}_{j = 1}h_j(x)] \end{aligned}$$

其中$\lambda \ge 0, \nu \ge 0$。上述拉格朗日对偶函数为什么只有两个参数$\lambda,\nu$了呢？因为$\inf$是将$L(x, \lambda, \nu)$取得最小值时对应的自变量的取值$x$代入进去，所得到的一个函数式子。此时的$f_0(x), g_i(x),h_j(x)$均为常量了，因此上式中只有两个参数，且为一个仿射函数。

拉格朗日对偶函数

根据上述描述，可以得知拉格朗日对偶函数是一个仿射函数，而任何一个仿射函数既是凸函数又是凹函数，所以可以将任意的标准形式的优化问题转换为与之对应的拉格朗日对偶函数问题。

Lower Bound Property

设$x^*$是原始问题$f_0(x)$的最优解，其函数值$f_0(x^*)$记为$p^*$，则对于任意的$\lambda, \nu$，有：$g(\lambda, \nu) \le p^*$，即：原始问题的最优解所对应的函数值是拉格朗日对偶函数的上确界。

可以将上述的性质理解为：拉格朗日对偶函数的函数值不会超过原始问题的最优解所对应的函数值。为什么这样说呢？上述性质是怎样来的呢？应该给出证明。设$\tilde{x}$是任意一个可行解，$\lambda \ge 0, \nu \ge 0$，$g_i(\tilde{x}) \ge 0, h_j(\tilde{x}) = 0$，有：

$$\begin{aligned} L(\tilde{x}, \lambda, \nu) &= f_0(\tilde{x}) + \lambda\sum^{m}_{i = 1}g_i(\tilde{x}) + \nu\sum^{n}_{j = 1}h_j(\tilde{x}), \lambda \ge 0, \nu \ge 0 \\ &= f_0(\tilde{x}) + \lambda\sum^{m}_{i = 1}g_i(x) \\ &\le f_0(\tilde{x}) \end{aligned}$$

又根据下确界的定义（可以将下确界从效果上大致理解为最小值，虽然它两个还有细微的差别，但是可以直观上这么理解，可以暂时将其理解为最小值定义），得到：

$$\begin{aligned} L(\tilde{x}, \lambda, \nu) \ge \inf_xL(x, \lambda, \nu) &=\inf_x[f_0(x) + \lambda\sum^{m}_{i = 1}g_i(x) + \nu\sum^{n}_{j = 1}h_j(x)] \\ &= g(\lambda, \nu) \end{aligned}$$

将上述不等式联立起来，即可得到：$g(\lambda, \nu) \le L(\tilde{x}, \lambda, \nu) \le f_0(\tilde{x})$。即：对于任意一个可行解，拉格朗日的最大值都不会超过原始问题的函数值。所以将$\tilde{x}$换为最优解$x^*$后，命题得证。

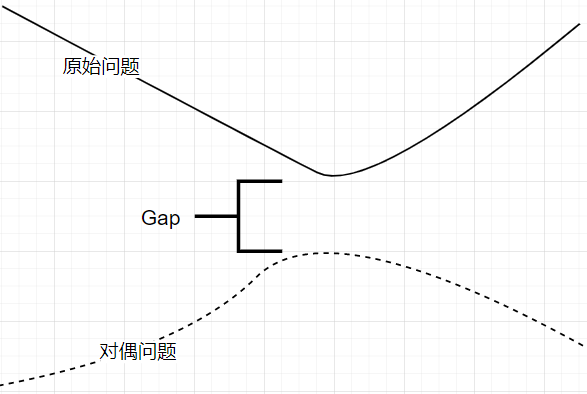
根据Lower Bound Property，求解原始问题的最优解，其实就是相当于求解拉格朗日对偶问题的最大值。由于对于仿射函数，它既是凸函数又是凹函数，所以我们倾向于将仿射函数看做是一个凹函数（因为大多数情况下都是凹函数求最大值，凸函数求最小值）。

所以**拉格朗日对偶函数构成了原始问题的最优点的函数值$p^* = f_0(x^*)$的下界。**而其最好的解就是与原始问题的最优解的函数值是相等的，但是也可能不会相等，那么什么时候相等，什么时候又不相等呢？这就需要一个新的判断标准，这就涉及到了Strong and Weak Duality.

Strong and Weak Duality

设$p^*$是Primal Optimal，$d^*$是Dual Optimal，则：

• $p^* \ge d^*$是一定成立的
• $p^* = d^*$是不一定成立的

对于$p^* = d^*$称为强对偶性（Strong Duality），而$p^* \ge d^*$称为弱对偶性（Weak Duality）。对于强对偶性来说：

• 一般情况下是不成立的
• 在凸函数下一般会成立
• 对于非凸函数来说，有时候会成立

对于强对偶性成立的优化问题来说，求得对偶问题的最优解后，不用再做调整，可以直接作为原问题的最优解来使用；而对于弱对偶性来说，还需要对对偶问题的解做一系列调整才能用作原问题的解。

那么到底什么时候，具有强对偶性呢？需要满足Slater’s Conditions.

Slater’s Conditons

对于一般优化问题的标准形式而言：

$$\begin{aligned} \min \quad &f_0(x) \\ s.t. \quad &g_i(x) &\le 0, &i = \{1, 2, 3, ..., m\} \\ &h_j(x) &=0, &j = \{1, 2, 3, ..., n\} \end{aligned}$$

如果存在可行解$\tilde{x}$，使得$g_i(\tilde{x})$严格小于0成立，$h_j(\tilde{x}) = 0$严格成立，*这个条件称为Slater条件*。

Slater定理 - 用来判断强对偶性是否成立

如果原始问题（Primal Problem）是凸优化问题，且Slater条件成立，则强对偶性成立。即：它描述的是：当Slater条件成立且原问题是凸优化问题时，强对偶性成立。

Complementary Slackness

假设强对偶性成立（Strong Duality），$x^*$是Primal Optimal，$\lambda^*, \nu^*$是Dual Optimal，根据Lower Bound Property有：

$$\begin{aligned} f_0(x^*) = g(\lambda^*, \nu^*) &= \inf_x[f_0(x) + \lambda^* \sum^{m}_{i = 1}g_i(x) + \nu^*\sum^{n}_{j = 1}h_j(x)] \\&\le L(x^*, \lambda^*, \nu^*) = f_0(x^*) + \lambda^*\sum^{m}_{i = 1}g_i(x^*) + \nu^*\sum^{n}_{j = 1}h_j(x^*) \\&\le f_0(x^*) \end{aligned}$$

即：$f_0(x^*) \le f_0(x^*)$。而要想左式成立，则必须要有$\lambda^*\sum^{m}_{i = 1}g_i(x) = 0$。又因为对于$g_i(x)$来说，每一项都是非正的，所有$\lambda^*\sum^{m}_{i = 1}g_i(x) = 0$等价于$\lambda^*g_i(x) = 0$

$$\begin{cases} \lambda^* =0, g_i(x) \le 0 \\ \lambda^* > 0, g_i(x) = 0 \end{cases}$$

也就是说：当强对偶性成立时，$x^*$是原问题的最优解，如果$\lambda^*, \nu^*$是对偶问题的最优解的必须满足的必要条件（上述的条件$\lambda^*g_i(x)=0$）称为互补松弛条件。