线性模型的基本形式

假设样本空间中的所有样本均服从某一分布，从样本空间中独立同分布的进行采样所得的样本集作为训练集。

线性模型指的是假设可以通过属性空间中的各个属性的线性组合所得到的预测函数对新样本进行预测，即对给定的新样本作为输入，用使用预测函数所得到的输出值作为新样本的真实值的预测。

设$\pmb{x}=\{x_1; x_2; \cdots; x_d\}$ 为具有d个属性的样本（也称实例），其中$x_i$ 代表的是样本$\pmb x$ 的第i个属性的取值。需要注意的是，$x_i$ 是一个样本所给定的标量值，它不是变量，且它是已知量而不是未知量。$\pmb W = \{w_1; w_2; \cdots; w_d\}$ 为权重列向量，其中$w_i$ 代表的是样本$\pmb x$ 的第i个属性的权重。根据上述假设和定义，可以得到线性模型的一般形式：

$$f(\pmb x) = w_1x_1 + w_2x_2 + \cdots + w_dx_d +b = \pmb w^T\pmb x + b$$

其中b 为偏置项，是一个标量。

NOTICE

• 线性模型指的是可以通过样本属性的线性组合作为预测函数对新样本的实际值进行预测。由于这个预测函数是线性的，故称该模型（映射关系）为线性模型。

• 上述线性模型中的未知量为$\pmb w, b$ ，已知量为$\pmb x$

线性回归

线性模型矩阵化和向量化

使用模型对实值进行预测，称该任务为回归任务；使用线性模型对实值进行预测，称为线性回归。

设数据集$D = \{(\pmb x_1, y_1), (\pmb x_2, y_2), \cdots, (\pmb x_m, y_m)\}$ 为从样本空间中独立同分布采样所得到的集合。其中$\pmb x_i = (x_{i1}; x_{i2}; \cdots; x_{id})$ 是由d个属性所描述的样本，$x_{id}$是第i个样本第d个属性的具体取值。

为了能够使用矩阵和向量的形式表示线性模型，将未知量（称为参数）吸收进一个列向量中$\hat{\pmb w} = (\pmb w; b)$ ，其维度为$d + 1$ ；对数据集D进行改造，设$\pmb X = (\pmb x, I)$，其中$I$是维度为d，值为全1的向量。则矩阵$X$ 的维数$m \times (d + 1)$，则有：

$$\hat{\pmb y} = f(X) = X\hat{\pmb w}$$

结果为一个向量值函数，即：$\hat{\pmb y}$是一个维度为m的列向量。

求解参数$\hat{\pmb w}$

线性回归模型的目标是：从给定数据集中学习得到一个线性模型，以使得实值输出与实际值的误差在某种度量下尽可能的小的那组参量（未知量）$\hat{\pmb w}$。线性回归中常用的误差度量为均方误差MSE。

设向量$\pmb y$ 为训练集的样本的实际值向量，维度为m。采用MSE作为度量标准后，可以将上述学习目标使用数学语言进行描述：

$$\begin{aligned} \hat{\pmb w}^*=\mathop{\arg\min}\limits_{\hat{\pmb w}}(y - X\hat{\pmb w})^T(y - X\hat{\pmb w}) \end{aligned}$$

由于目标函数是高维度的凸函数，可以使用求导的方式获得其解析解。设：$E=(y - X\hat{\pmb w})^T(y - X\hat{\pmb w})$，对其展开有：

$$\begin{aligned} E &= (y - X\hat{\pmb w})^T(y - X\hat{\pmb w}) \\ &= y^Ty -y^TX\hat{\pmb w} - \hat{\pmb w}^TX^Ty + \hat{\pmb w}^TX^TX\hat{\pmb w} \end{aligned}$$

对参数$\hat{\pmb w}$求偏导，有：

$$\begin{aligned} \frac{\partial E}{\partial \hat{\pmb w}} &= \frac{\partial E}{\partial \hat{\pmb w}}(y^Ty -y^TX\hat{\pmb w} - \hat{\pmb w}^TX^Ty + \hat{\pmb w}^TX^TX\hat{\pmb w}) \\ &=0 - X^Ty - X^Ty + (X^TX + X^TX)\hat{\pmb w} \\ &= 2X^T(X\hat{\pmb w} - y) \end{aligned}$$

令$\frac{\partial E}{\partial \hat{\pmb w}} = 0$，有：

$$2X^T(X\hat{\pmb w} - y) = 0 \to X^TX\hat{\pmb w} = X^Ty$$

若矩阵$X^TX$ 可逆，（即满秩），则可以得到关于参数$\hat{\pmb w}$的解析解：$\hat{\pmb w}= (X^TX)^{-1}X^Ty$ ，其中$X, y$均为已知量。

如果矩阵$X^TX$不可逆，则常用的方法为对采用MSE度量加上一个正则化项，在避免模型过于复杂的同时还可以使得最有求解参数$\hat{\pmb w}$时的矩阵为可逆矩阵。

而对于上述解析解的求解，可以使用数值分析里面的方法进行求解。

对数几率回归

对数几率回归的本质

对数几率回归，也叫逻辑斯蒂回归，它的目的是对离散值的预测，它是一个二分类的学习器。所谓的对数几率回归只是将线性回归的实值输出再做一次映射，从实值空间到分类空间的映射。

阶跃函数$sgn(x)$可以将实值压缩为$0, 1$离散值。即：

$$sgn(x) = \begin{cases} 1 & x > 0.5 \\ 0.5 & x = 0.5 \\ 0 & x < 0.6 \\ \end{cases}$$

但是阶跃函数是一个不光滑的分段函数，其函数性质较差，因此需要选择一个光滑的函数来阶跃函数进行替代，sigmoid 函数就应运而生：

$$y = \frac{1}{1 + e^{-x}}$$

其图像为：

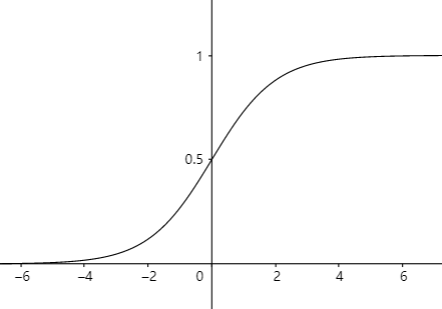
可以看出sigmoid函数可以将实值空间映射到（压缩到）$(0, 1)$区间上。该函数光滑，且只有在正无穷或负无穷处取得1或者0值。

使用sigmoid函数作为线性回归实值输出到分类空间的非线性映射，有：

$$y = \frac{1}{1 + e^{-(\pmb w^T\pmb x + b)}}$$

整理上式，有：

$$\ln\frac{y}{1 - y} = \pmb w^T\pmb x + b$$

由于sigmoid函数满足概率的公理化定义，可以将$y$理解为正例所出现的概率（即：标签为$+1$对应的样本为正例，$0$对应的样本为反例） ，则$1 - y$可以理解为反例所出现的概率。则$\frac{y}{1-y}$描述的是正例所出现的相对概率，称为几率；而$\ln\frac{y}{1 - y}$描述的是正例所出现的对数几率。这也就是为啥该模型称为对数几率回归。

对数几率模型的数学描述

根据上一节，可以得知$y$为正例所出现的概率，$1 - y$为反例所出现的概率，即：

$$y = p(y = 1|\pmb x; \pmb w, b) = p_1(\pmb x; \pmb w, b) \\ 1 - y = p(y = 0 | \pmb x; \pmb w, b) = p_0(\pmb x; \pmb w, b)$$

带入$\ln\frac{y}{1 - y} = \pmb w^T\pmb x + b$ ，有：

$$\begin{aligned} &\ln\frac{p_1(\pmb x; \pmb w, b)}{1- p_1(\pmb x; \pmb w, b)} = \pmb w^T\pmb x + b \\ &\Rightarrow p_1(\pmb x; \pmb w, b) = \frac{e^{ \pmb w^T\pmb x + b}}{1 + e^{ \pmb w^T\pmb x + b}} \\ &\Rightarrow p_0(\pmb x; \pmb w, b) = \frac{1}{1 + e^{\pmb w^T\pmb x + b}} \end{aligned}$$

求解参数$\pmb{w}, b$

令$\beta = (\pmb w; b)$， $z = (x; 1)$，则上述公式可以改写为：

$$\begin{aligned} &\ln\frac{p_1(\pmb x; \pmb w, b)}{1- p_1(\pmb x; \pmb w, b)} = \beta^Tz \\ &\Rightarrow p_1(\pmb x; \pmb w, b) = \frac{e^{\beta^Tz}}{1 + e^{\beta^Tz}} \\ &\Rightarrow p_0(\pmb x; \pmb w, b) = \frac{1}{1 + e^{\beta^Tz}} \end{aligned}$$

其中未知量为$\beta$ 。学习目标为：使得预测的分类的概率尽可能为正确分类值。使用极大似然估计来估计最优参量。

构造对数似然函数：

$$\mathbb{L}(\beta) = \sum_{i = 1}^m \ln p(y_i|z_i; \beta)$$

而$p(y_i|z_i; \beta)$可以由

$$p(y_i|z_i; \beta) = y_ip_1(\pmb x; \pmb w, b) + (1 - y_i)p_0(\pmb x; \pmb w, b)$$

所表示。原因是由于是2二分类问题，真实值只可能是0或者1，带入上式后可以将分段函数合并成一个函数表达式。将该函数表达式代入对数似然函数有：

$$\begin{aligned} \mathbb{L}(\beta) = \sum_{i = 1}^m (\ln(y_ie^{\beta^Tz_i} + 1 - y_i) - \ln(1 + e^{\beta^Tz_i})) \end{aligned}$$

由于$y_i$的可能取值只有0和1，则$\ln(y_ie^{\beta^Tz_i} + 1 - y_i) - \ln(1 + e^{\beta^Tz_i})$可以拆为分段函数：

$$\begin{cases} - \ln(1 + e^{\beta^Tz_i}) & y_i = 0 \\ \beta^Tz_i - \ln(1 + e^{\beta^Tz_i}) & y_i = 1 \end{cases}$$

上述分段公式又可以根据技巧何为一个函数表达式：

$$y_i(\beta^Tz_i - \ln(1 + e^{\beta^Tz_i})) - (1 - y_i)\ln(1 + e^{\beta^Tz_i})$$

则对数似然函数可以写为：

$$\begin{aligned} \mathbb{L}(\beta) = \sum_{i = 1}^m (-y_i\beta^Tz_i + \ln(1 + e^{\beta^Tz_i})) \end{aligned}$$

上述对数似然函数是凹函数，对对数似然函数取反，则最大化似然函数变为最小化似然函数，即：

$$\beta^*=\mathop{\arg\max}\limits_{\pmb \beta}\mathbb{L}(\beta)= \mathop{\arg\min}\limits_{\pmb \beta}-\mathbb{L}(\beta)$$

可以使用数值分析中的方法进行求解。