标量、向量和矩阵

定义

标量（scalar） 一个标量就是一个单独的数，用斜体表示标量，例如​x \in \mathbb{R}
向量（vector） 一个向量就是一列数，可以视为一维数组，用粗体的小写变量名称表示向量，例如​\pmb{x} \in \mathbb{R}^{n}，如果无特殊说明，给定的向量默认为列向量，即：

矩阵（matrix） 矩阵是一个二维数组（表），用粗体大写变量名称表示矩阵，例如​\pmb{A}\in \mathbb{R}^{m \times n}。一个矩阵可以表示如下：

符号约定

采用不同字体区分标量、向量和矩阵：

• 用小写字母斜体表示标量（scalar）
• 用小写字母、斜体加粗表示向量（vector）
• 用粗体大写字母表示矩阵（matrix）

注意，向量可以表示标量，例如​\pmb{x}(1)表示一个标量；矩阵可以表示向量或标量，例如​A(1,1)是一个标量，​A(1)是一个列向量。

矩阵求导

不同的文献中，同样的式子求导的结果有时候会不一样，仔细观察会发现刚好相差一个转置。例如文献1：

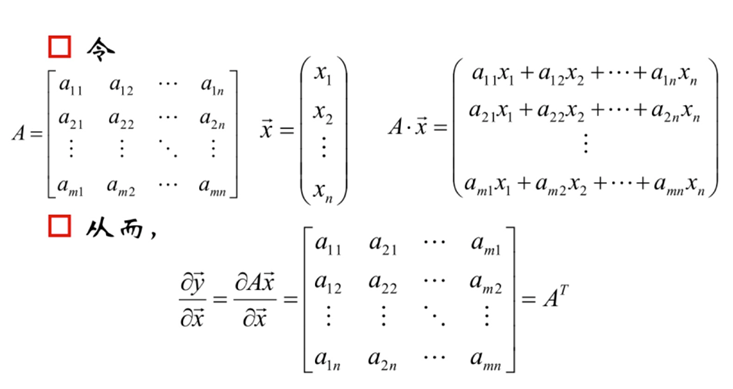
文献2：

上述两者结果就互不相同。

矩阵求导的本质

矩阵函数求导的本质是对函数中的映射关系逐一对变元求偏导后，然后写成向量或矩阵表达的形式。例如数量值函数：

可以对​f分别对变量​{x}_{1}, {x}_{2}, {x}_{3}求偏导，有：

需要注意的是，矩阵求导中的函数可以是数量值函数，也可以是向量值函数。因此，​f表示的是一个映射关系，一个函数可以有多个映射关系​f。例如数量值函数只有一个映射关系​f，而向量值函数可以有​n个映射关系​f_{1}, {f}_{2}, \cdots, f_{n}。

布局约定

针对例子​f({x}_{1}, {x}_{2},{x}_{3}) = {x}_{1}^{2}+{x}_{1}{x}_{2} + {x}_{2}{x}_{3}，其对向量​\pmb{x} = ({x}_{1}, {x}_{2}, {x}_{3})^{\top}求导的结果在写成矩阵的形式时，有两种不同的选择，分别是将其结果表达为列向量的形式，即：

或表示为行向量的形式，即：

总结这两种表示形式的规律后，可以发现一个是保持分子表示形状不变，分母变为原来转置的形状；另一个是保持分母表示形状不变，分子变为原来转置的形状。分别称他们为分子布局和分母布局。通常情况下，分子布局和分母布局的结果互为转置。

分子布局

分子布局指的是保持求导结果中分子表示方法不变，分母变为原来的转置形式。

分母布局

分母布局指的是保持求导结果中分母表示方法不变，分子变为原来的转置形式。

混合布局

在机器学习算法理论中，并没有看到说正在使用什么布局，也就是说布局被隐含了，需要自己推理，但是一般来说，我们会使用一种叫混合布局的思路：

• 向量或者矩阵对标量求导，则使用分子布局
• 标量对向量或者矩阵求导，则使用分母布局
• 向量对向量，有些分歧，一般多使用分子布局的雅克比矩阵混合布局遵守的原则是改变简单形式的形状，保持复杂形式的形状不变。

混合布局遵守的原则是改变简单形式的形状，保持复杂形式的形状不变。

求导三条规则

链式法则、加法规则和乘法规则对于矩阵求导同样适用。即：

1. 链式法则：​\frac{\mathrm{d}z}{\mathrm{d}x} = \frac{\mathrm{d}z}{\mathrm{d}y} \cdot \frac{\mathrm{d}y}{\mathrm{d}x}
2. 加法法则：​\frac{\mathrm{d}(au + bv)}{\mathrm{d}x} = a\frac{\mathrm{d}u}{\mathrm{d}x} + b\frac{\mathrm{d}v}{\mathrm{d}x}
3. 乘法法则：​\frac{\mathrm{d}(uv)}{\mathrm{d}x} =v\frac{\mathrm{d}u}{\mathrm{d}x} + u \frac{\mathrm{d}v}{\mathrm{d}x}

雅可比矩阵

在向量分析中，雅可比矩阵（也称作Jacobi矩阵，英语：Jacobian matrix）是函数的一阶偏导数以一定方式排列成的矩阵，其为向量对向量求导，采用的是分子布局，即：

参考资料

• Matrix_calculus#Scalar-by-vector_identities
• The Matrix Cookbook.pdf