凸集合

什么是“凸性”？

“凸”是一个几何性质，其描述的可以几何图形的边界上的点在某一个方向上不低于其周围点。也可以换个角度，从整体出发描述几何图形向四周鼓出。

定义凸集

由于第一个定义涉及到多个数学概念的定义，在实际操作中比较复杂，因此选择第二个定义（即“四周鼓出”）来对集合的凸性进行定义。

对于“四周鼓出”的凸图形来说，图形中任意两点的直线段仍然在该图形内，将该描述转化为数学语言，有：集合C中任选两点\pmb{x}, \pmb{y}，对于任意参数\alpha \in [0, 1]，有\alpha \pmb{x} + (1 - \alpha)\pmb{y} \in C，则称该集合是凸集。

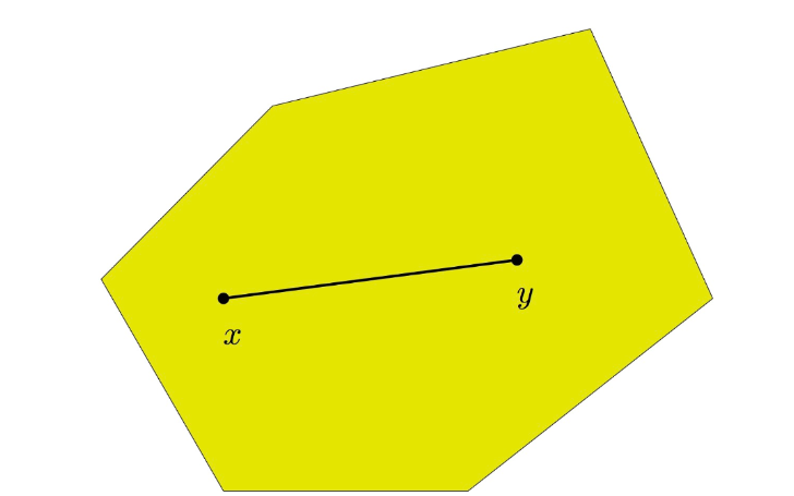
证明：以点\pmb{y}为起点，\pmb{x}为终点的直线段的表示形式为\alpha \pmb{x} + (1 - \alpha)\pmb{y}, \alpha \in [0, 1].

从起点y指向终点\pmb{x}的方向为

由于为直线段，则可以引入闭区间[0, 1]内的参数\alpha，有：

整理，有：

凸包与凸组合

凸组合指点的线性组合，要求所有系数都非负且和为 1，点集的凸包等价于该点集的所有凸组合。

一个凸集的凸包就是它自己，一个非凸集A的凸包则是这样产生的：

1. 把A中的点都用线段连接起来，形成一个新集合
2. 如果形成的新集合A还不是凸集，继续再对这个新集合进行同样的过程，则又形成一个集合
   如此反复，直到最后形成的集和是凸集，这个凸集就是A的凸包。

假设有平面上三个点所构成的凸包，现考虑这个三角形中的点的表示，设三个点为{x}_{1}, {x}_{2},{x}_{3}\in \mathbb{R}^{2}，则三条边上的点由定义可表示为：

其中\lambda_{i} \in [0, 1], i = 1,2, 3。而三角形内部的点是由上述形式的两个点来表示的，例如：

代入x_{{\lambda}_{1}}, x_{{\lambda}_{2}}，有：

其中：

且满足\bar{\lambda}_{i} > 0, i = 1, 2, 3; \bar{\lambda}_{1} + \bar{\lambda}_{2} + \bar{\lambda}_{3} = 1。

常见的凸集

• 实数空间\mathbb{R}^{n}
• 所有正数集合\mathbb{R}_{+}^{n}
• 范数||\pmb{x}|| \leq 1
• 仿射集：线性方程组的所有解\pmb{A}\pmb{x} = \pmb{b}
• 半空间：不等式的所有解\pmb{A}\pmb{x} \leq \pmb{b}

一些有用结论

下面不加证明地给出一些常用结论：

1. 凸集的交集仍然是凸集
2. 每一个多面体都是一个凸集。注意：多面体是有限个超平面和半空间的交集。
3. 一个凸集中的有限个元素的凸组合仍然属于该集合
4. 由有限向量组成的凸包是一个凸集。
5. 若\pmb{w}为凸函数，由多个不等式构成的集合C：\{w|g(w) \leq a\}为凸集

具体证明见Boyd的Convex Optimization教材。

凸函数

要用几何方法来研究函数，最自然的办法就是给出函数的集合表示，即通过函数的图像来研究函数的性质。一个单变量函数的图像通常是平面上的一条曲线，而一条曲线一般是不会构成一个凸集的，除非这条曲线是直线或直线段。为了能运用凸性理论来研究函数，应设法把函数的图像加厚，使得原来的图像成为加厚过图像的一部分边界。

函数的上图

设f:(a, b) \mapsto \mathbb{R}为定义在\mathbb{R}中的开区间(a,b) := \{x \in \mathbb{R}|a < x< b\}上的实值函数，这里a,b满足-\infty \leq a < b \leq +\infty，则集合

称为函数f的上图(epigraph)。根据函数f的上图定义可知，函数的上图就是函数的图像再并上图像上方所有点。

凸函数的定义

如果函数f: (a,b) \mapsto \mathbb{R}的上图\mathrm{epi}f是凸集，则称f为(a,b)上的凸函数。如果这时f的图像上的点都是\mathrm{epi}f的严格凸点，则称f为(a,b)上的严格凸函数。

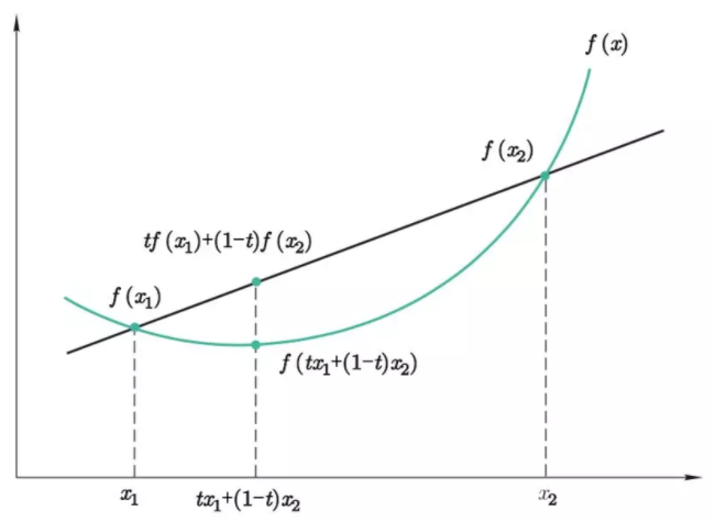
根据凸函数的定义，可以导出凸函数的充要条件：对于函数定义域\mathrm{dom}f内的任意两点\pmb{x}, \pmb{y}，对于任意实数t \in (0, 1)，满足

凸函数定义的几何意义：凸函数的割线总在函数曲线的上方。

判定凸函数

凸函数定义

利用凸函数的定义来判断给定函数是否为凸函数。

举个例子，证明所有的欧几里得范数均为凸函数，即

是凸函数。首先，其定义域为\pmb{w} \in \mathbb{R}^{d}为凸集。其次，根据p范数定义，有：

其中p \geq 1。任取\pmb{x}, \pmb{y} \in \mathbb{R}^{d}，\alpha \in (0, 1)，有：

一阶条件

考虑一个可微函数f，即f的梯度\nabla f在其定义域\mathrm{dom}f中处处存在，函数f是凸函数当且仅当对于\forall x, y \in \mathrm{dom}f，有下式成立：

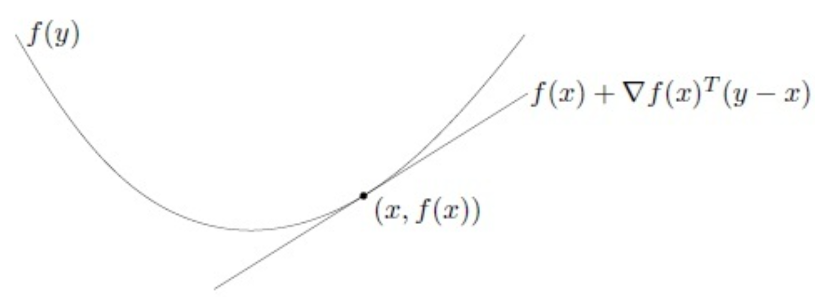
凸函数的一阶判定条件的几何含义：凸函数永远位于其切线的上方。

二阶条件

现在我们假设函数f是二阶可微的，即函数f的Hessian矩阵在定义域内处处存在，那么函数f是凸函数当且仅当对于定义域内的任意一点\pmb{x}，该点处的Hessian矩阵是半正定的，即：

对于标量函数而言，Hessian矩阵半正定退化为：f''(x) \geq 0，意味着函数f的导函数是非递减的。从几何上来说，Hessian矩阵处处半正定意味着函数f处处曲率非负。

保凸运算

如果函数f和g均为凸函数，以下操作之后仍然是凸函数：

• 非负放缩：h(\pmb{w}) = af(\pmb{w})
• 加和：h(\pmb{w}) = f(\pmb{w}) + g(\pmb{w})
• 最大值：h(\pmb{w}) = \mathrm{max}\{f(\pmb{w}), g(\pmb{w})\}，一般可以用最大值函数将绝对值符号去掉，如|x| = \mathrm{max}\{x, -x\}
• 仿射变换：h(\pmb{w}) = f(\pmb{Aw} + \pmb{b})

但是一般情况下，复合函数f(g(\pmb{w}))不是凸函数。

凸优化问题

凸优化问题定义

考虑如下优化问题：

当且仅当：

• 目标函数f(x)是凸函数
• 可行域C（即参数x的可行解空间）是凸集
  该优化问题是凸优化问题。

凸优化问题的重要性质：局部最优解即是全局最优解

凸优化问题有一个关键的性质：所有的局部最优解均是全局最优解。

证明：定义域为C的凸函数f(x)的局部最优解x^{*}是全局最优解。

利用反证法。假设x^{*}是局部最优解不是全局最优解，则一定存在有一点y \in C，使得

由于定义域C是凸集，则对任一实数t \in (0, 1)，可构造一新点z，有：

进而有：

即：f(z) < f(x^{*})。矛盾出现，上式表示在x^{*}的邻域内存在有一点比局部最小值点x^{*}更小，故假设不成立，命题得证。