高级数据结构:B树的拆解与实现
编辑
为什么需要多叉树?
二叉树存在的问题
现有的计算机一般都会有经典的三级存储:CPU、内存和磁盘。其中,CPU中的缓存访问速度最快,内存次之,磁盘最慢。
假设二叉树中的每个节点存储的是磁盘页的话,那么每次查找到二叉树中的一个节点时,都会产生一次磁盘寻址。而一旦数据量很大时,这棵二叉树的高度也会随之增大,从而增加了访问节点时的磁盘寻址次数,这是非常耗时的,这就产生了一个降低树层高的数据结构的需求以加速查找效率。
最简单的降低树高的想法,就是增加节点中保存的数据的数量,由二叉树中只保存一个数据扩展为可以保存多个数据,从而同样数量的数据,构成的一棵树的树高会降低很多,多叉树的数据结构就自然而然的产生了。
多叉树
所谓的多叉树,指的是树中的任一分支节点,其子节点数大于2,节点中保存的数据个数m = n - 1,其中n为当前节点的子节点个数。树中所有分支节点中的最大子节点数(分支数)被定义为该多叉树的阶。即n阶多叉树指的是最大分支节点的子节点数为n。
多叉树与B树
n阶多叉树仅约束了树中的任一分支节点的最大分支数及节点中保存的数据个数,对于树的平衡性并没有约束。当树的平衡性较差时,其查找效率就会大幅度的降低。
B树本质上是一棵带有约束的多叉树,其要求该棵多叉树是平衡多叉排序树。
B树定义
满足以下性质的M阶多叉树即为一棵B树:
- 每个节点至多有M棵子树
- 根节点如果有子树,则根节点至少有2棵子树
- 除根节点以外,其它分支节点至少有\lceil \frac{M}{2} \rceil个子树
- 有k棵子树的分支节点则存在有k - 1个关键字,关键字按照递增/递减顺序存储
- 分支节点中的关键字数量满足\lceil \frac{M}{2} \rceil - 1 \le n \le M - 1,其中n为关键字数量
- 所有的叶子节点均在同一层
根据上述定义可以看出,其限制了根节点、分支节点和叶子节点:
- 限制根节点的子树的数量
- 限制分支节点的:
- 关键字数量和子树数量
- 关键字存储顺序
- 限制叶子节点的层次必须相同
B树理论上如何保持平衡性?
根据上述B树的性质,其中最关键的一条要求:所有叶子节点必须处于树中的同一层次上。满足了这一条性质,则从根节点到叶子节点的所有路径上的节点数量是相同的,从而也就保证了这棵多叉树的平衡性。
B树的增删改查
假设树中节点的关键字按照递增的顺序存储的。下面的图示为了绘制方便,对于 key-value 存储的,只绘制出 key。
B树的定义
节点定义
template <typename _Tk, typename _Tv=int> // _Tv暂时保留
struct _btree_node {
using key_type_t = _Tk;
// 索引值数组
key_type_t *keys = nullptr;
// 分支数组
struct _btree_node **children = nullptr;
struct _btree_node *parent = nullptr;
// 节点中的关键字数量
size_t num = 0;
// 当前节点是否是叶子节点
bool leaf = false;
};
采用数组存储节点内部的关键字,为了实现方便,并没有指定 value,而是仅保存了 key。
树的定义
template <typename T>
class btree {
using key_type_t = T;
public:
using btree_node = struct _btree_node<key_type_t>;
private:
btree_node *root = nullptr;
// m阶B树的最小分支数,通过最小分支数可以定义最大分支,不用做除法和取整操作
const size_t minimum_branches = 3;
const size_t maximum_branches = 2 * minimum_branches;
};
查找
节点内部查找
由于节点中的关键字是按序排列的,因此可以使用综合的查询方式进行查询。当长度很长时可以使用二分查找进行查找;当缩小到一定程度时,使用线性搜索进行查找。
下面代码示例采用的是线性搜索,未使用综合策略,仅做原理上的实现。
template <typename T>
size_t btree<T>::linear_find(const btree_node *node, const key_type_t& key) const {
const btree_node *cursor = node;
size_t idx = 0;
while (idx < cursor->num && cursor->keys[idx] < key) ++idx;
// 返回的是在当前给定节点内部的索引值,cursor->kesy[idx] >= key
return idx;
}
查找节点
查找节点的方式与二叉排序树的查找方式是类似的,只不过添加了一些额外的操作以适应多叉树:
- 当某一节点内部包含有该
key值,则直接返回该节点及其在该节点内部的索引下标; - 如果上述节点内部不包含这个
key值,则查找到第一个大于给定key值的索引。由于节点内部的关键字是按照递增策略进行存储的,因此查找到的索引就是其下一个要查找的节点在分支节点数组中的下标索引值。
查找节点的示例代码如下:
template <typename T>
typename btree<T>::btree_node*
btree<T>::find(const key_type_t &key, size_t& index) const {
// 1. 空树时,直接返回空
if (!root) {
return nullptr;
}
btree_node *cursor = root;
while (cursor) { // 从根节点开始查找
size_t idx = linear_find(cursor, key);
// 如果当前的值正好是要查找的key
if (idx < cursor->num && cursor->keys[idx] == key) {
index = idx; // 返回这个key在当前游标节点中的下标索引
return cursor;
}
// 否则就是idx == cursor->num || cursor->keys[idx] > key
// 这两个分支可以合并为一个进行处理
cursor = cursor->children[idx];
}
return nullptr;
}
查找图示
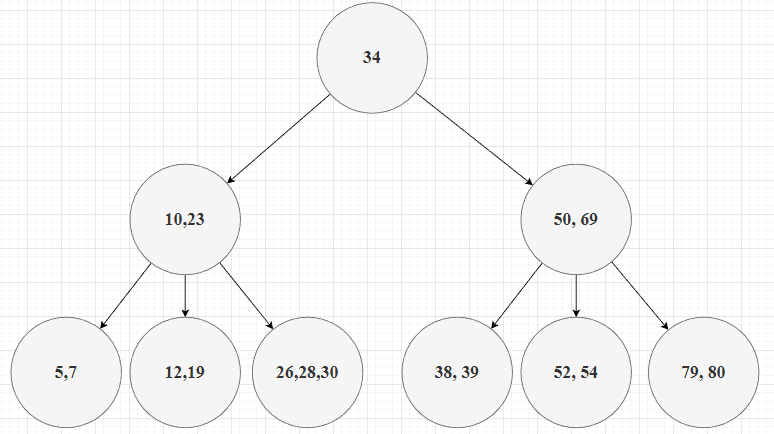
假设有一棵4阶B树如下图所示:

现要查找元素19:
- 首先,从根节点34出发,发现其小于34,此时的索引值为0,则下一个要查找的节点位于分支节点数组中的第0号位置,左子树上的节点
[10,23] - 然后,流程转移到节点
[10, 23],发现其小于23,此时的索引值为1,则下一个要查找的节点位于分支节点数组中的第1号位置,即中间节点[12, 19] - 最后,流程转移到叶子节点
[12, 19],发现存在键值19,故直接返回该叶子节点的指针,并返回在该节点中键值19所对应的下标索引号1。
插入
为了保证叶子节点位于同一层次,即自平衡性。当打破了B树的性质5关键字数量限制这一条性质时,应采取分裂动作,从而可以保证叶子节点始终位于同一层次。
插入 A-Z示意
设当前B树为6阶B树,现插入 A-Z字母到该棵树中。
由于B树是6阶的,则一个节点中最多可以容纳的关键字数量为5个。因此,当当前B树为空时,可以直接向其内部插入5个字母A-E。当要插入F时,发现当前根节点的关键字个数大于5了,因此需要分裂。
由于节点内部的关键词的是以递增顺序存储的,因此可以将节点中的中间元素提取出来,作为其父节点中的关键字,而在其两侧的关键字分裂为两个节点,作为其孩子节点即可,如下图所示:
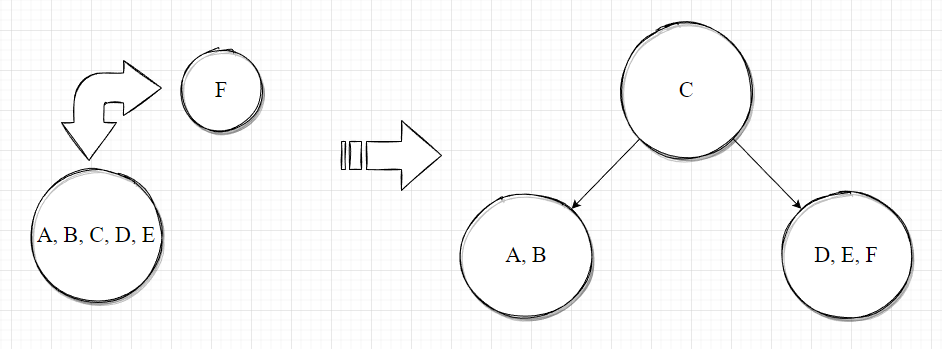
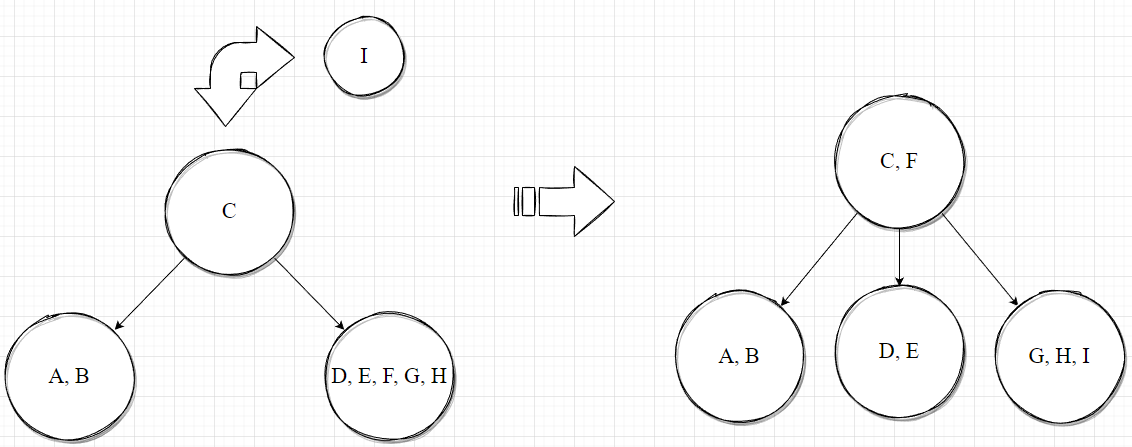
然后插入元素 F即可。同理,在插入到元素 I时,发现右孩子节点所能插入的索引值个数已满,因此需要分裂后再插入。
剩余的元素的插入如下列图示:
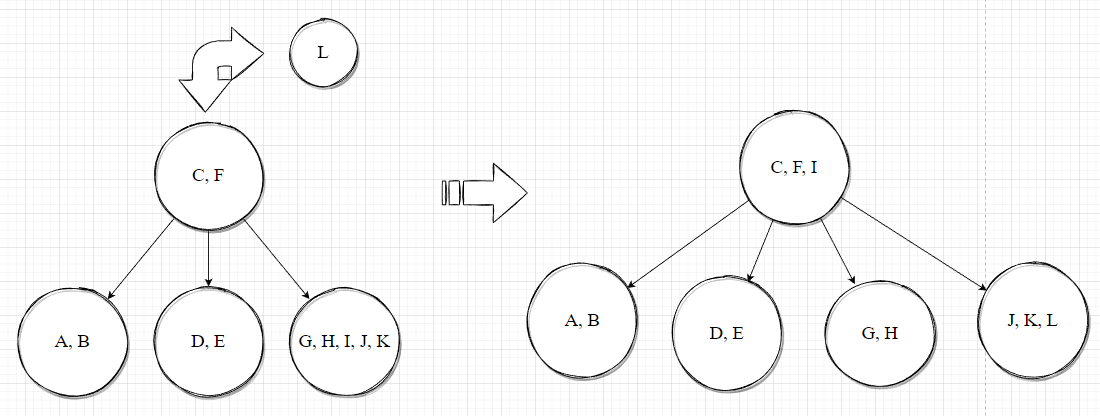
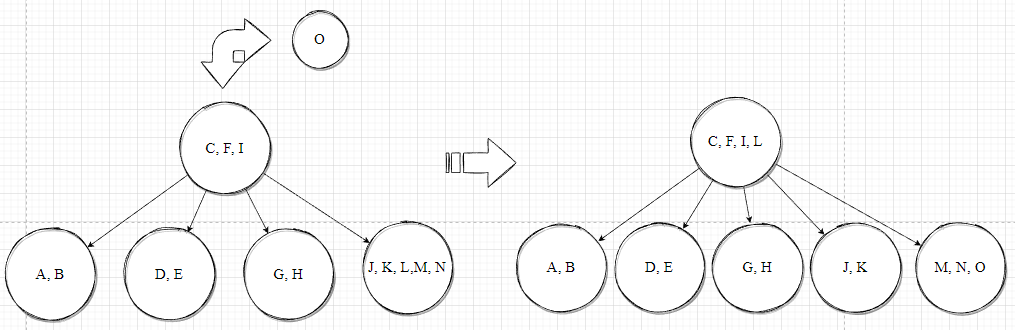

注意,当插入 U时,树中此时有两个节点中存储的元素个数达到上限,应依据先碰到哪个达到索引存储上限的节点,哪个节点先分裂,分裂完毕后再向下寻找插入的,以避免后续节点需要分裂而父节点没有足够的位置导致无法分裂的情况。


最后,插入完成后的B树如下图所示:

插入操作实现
主逻辑
主插入逻辑如下:
template <typename T>
void btree<T>::insert(const key_type_t &key) {
btree_node *cursor = root;
if (cursor->num == maximum_branches - 1) {
// 需要分裂到可以插入的状态后,插入当前索引值
// 注意:分裂只在插入时会出现
btree_node *node = create_node(false);
assert(node != nullptr);
// 1. 先将当前新创建的节点作为父节点,当前cursor所指向的节点作为其第一个分支
node->children[0] = cursor;
cursor->parent = node;
root = node;
// 2. 分裂为两个子节点
split_children(node, 0);
// 3. 查找要插入的是哪个分支节点
// 注意,这里由于是提升父节点,因此父节点只可能分裂为两种
size_t idx = (node->keys[0] < key ? 1 : 0);
insert(node->children[idx], key);
return;
}
// 不需要分裂,可以直接插入
insert(cursor, key);
}
如果当前要分裂的是根节点,需要特殊处理一下。因为有一个根指针,也就是先创建一个新节点,并移动根节点指针到新创建的节点,将之前的根节点作为新根节点的最左孩子即可进入通用分裂节点逻辑进行处理了。
在主逻辑中调用了一个重载的 insert函数,其功能是在给定节点插入键值 key:
template <typename T>
void btree<T>::insert(btree_node *node, const key_type_t &key) {
size_t cursor = node->num;
// 1. 递归基,如果插入的是叶子节点,则直接插入即可
if (node->leaf) {
// 1. 先查找插入位置
while (cursor > 0 && node->keys[cursor - 1] > key) {
// 2. 将当前要插入的位置后的元素向后移动一个位置
node->keys[cursor] = node->keys[cursor - 1];
--cursor;
}
// 3. 将元素插入进去
node->keys[cursor] = key;
node->num++;
return;
}
// 2. 如果不是叶子节点,则当前要插入的位置是分支节点,其插入位置应该是其孩子节点
// 2.1 先找到要插入的位置
while (cursor > 0 && node->keys[cursor - 1] > key) {
--cursor;
}
// 2.2 如果要插入的孩子节点存储的元素已经达到上限,则需要先分裂后,再插入到其子孩子节点中
if (node->children[cursor]->num == maximum_branches - 1) {
split_children(node, cursor);
// 由于上来了一个新的key,需要再比较一下大小
cursor = (node->keys[cursor] < key ? cursor + 1 : cursor);
}
// 2.3 递归处理,直到插入的节点是叶子节点,从而直接插入即可
insert(node->children[cursor], key);
}
分裂操作
在插入的主逻辑中,其最重要的是 split_children函数,其实也很简单:
template <typename T>
void btree<T>::split_children(btree_node *parent, size_t index_in_parent) {
size_t neighbor_branch_index = index_in_parent + 1;
// 1. 将当前节点的中间值上升到父节点中
btree_node *current = parent->children[index_in_parent];
// 2. 创建新节点,并将当前节点中间键值右侧的全部拷贝到新节点中
btree_node *node = create_node(current->leaf);
assert(node != nullptr);
node->parent = parent;
size_t middle_key_index = minimum_branches - 1;
for (size_t i = 0; i < middle_key_index; ++i) {
node->keys[i] = current->keys[i + middle_key_index + 1];
}
// 如果不是叶子节点,需要将对应的分支拷贝出来
if (!current->leaf) {
// 需要注意的是,如果不是叶子节点,此时分裂时,还有最右一个分支,因此要多拷贝一个
for (size_t i = 0; i <= middle_key_index; ++i) {
// 3. 将当前节点中间键值右侧的所有孩子节点全拷贝到新节点中
btree_node *child = current->children[i + middle_key_index + 1];
node->children[i] = child;
child->parent = node;
}
}
// 4. 修改旧节点的键值数,修改新节点的键值数
current->num = middle_key_index;
node->num = middle_key_index;
// 5. 将父节点中的关键字向后移动
for (size_t i = parent->num; i > index_in_parent; --i) {
parent->keys[i] = parent->keys[i - 1];
}
// 6. 新节点作为父节点的新的一个分支
const key_type_t &middle_key = current->keys[middle_key_index];
parent->keys[index_in_parent] = middle_key;
parent->children[neighbor_branch_index] = node;
parent->num++;
}
其实逻辑上就是一个单独的节点,分为两个节点,并将分裂前的中间节点的键值上升到父节点中,并将分裂的两个节点作为其父节点的孩子节点即可。
修改
对于修改来说,如果要修改的是索引值的对应的值,可以利用上面已经阐述过的查找进行查找后修改;如果要修改的是键值,则需要先删除该键值,然后再插入新键值即可,即删除和增加两个函数的配合即可,故不在赘述。
删除
删除操作也可能会使得当前的多叉树违反B树的性质,因此在删除的时候如果违反了B树性质就需要进行调整。删除一个节点中的元素后,调整时可能会有以下几种情况:
- 当前节点中的元素个数位于[\lceil \frac{M}{2} \rceil -1, M - 1)之间,此时不需要调整
- 当前节点中的元素个数小于\lceil \frac{M}{2}\rceil - 1:
- 当前节点的左兄弟中的元素个数大于\lceil \frac{M}{2} \rceil - 1,即:其左兄弟可以借位一个元素补充到自身从而满足B树的性质。此时,只需要以其父节点为支点进行右旋,将左兄弟中的最大值上升到父节点,而父节点的值下降到当前节点中。
- 当前节点的右兄弟中的元素个数大于\lceil \frac{M}{2} \rceil - 1 ,即:其右兄弟可以借位一个元素补充到自身从而满足B树的性质。此时,只需要以其父节点为支点进行左旋,将右兄弟中的最小值上升到父节点,而父节点的值下降到当前节点中。
- 当前节点的左右兄弟中的元素个数均为\lceil \frac{M}{2} \rceil - 1,即:其左右兄弟均不可以借位。此时只需要将当前节点、父节点和其左兄弟或右兄弟合并成一个新的节点,然后以新的节点作为新的当前节点,递归向上调整即可。
而对于删除操作的语言描述1为:
删除操作是指,根据
key删除记录,如果B树中的记录中不存对应key的记录,则删除失败。1)如果当前需要删除的
key位于非叶子结点上,则用后继key(这里的后继key均指后继记录的意思)覆盖要删除的key,然后在后继key所在的子支中删除该后继key。此时后继key一定位于叶子结点上,这个过程和二叉搜索树删除结点的方式类似。删除这个记录后执行第2步2)该结点
key个数大于等于\lceil \frac{M}{2} \rceil - 1,结束删除操作,否则执行第3步。3)如果兄弟结点
key个数大于\lceil \frac{M}{2} \rceil - 1,则父结点中的key下移到该结点,兄弟结点中的一个key上移,删除操作结束。否则,将父结点中的
key下移与当前结点及它的兄弟结点中的key合并,形成一个新的结点。原父结点中的key的两个孩子指针就变成了一个孩子指针,指向这个新结点。然后当前结点的指针指向父结点,重复上第2步。
具体删除示例如下一小节,假设删除的树是插入小节中所建成的 A-Z的B树。
删除 Z-A示意
由于是六阶B树,故除根节点外至少有2个元素,因此在删除 Z-X时,由于其位于叶子节点中,可以直接删除。

而当删除 W时,虽然其是叶子节点,但是其元素个数已经到达下限,且其左兄弟中的元素也是下限,无法借位,因此需要和父节点中的元素 U合并成一个新的节点,并作为其父节点的新的节点,然后再删除元素 W,即如下所示:

然后继续删除元素 U, V ,由于不违反B树性质且待删除的元素在叶子节点上,故可以直接删除。当删除元素 T时,由于其达到了当前节点的元素个数下限且其左兄弟节点无法借位,故和其左兄弟节点和父节点中的元素 R合并成一个新的节点后删除元素 T。

同理,删除元素 SR,此时的树的形状为:

此时,删除元素 Q,可以发现其左孩子不可以借位,父节点中的元素 O如果和 MN及 PQ合并成一个节点的话,父节点 LO会违反除根节点以外,其它任一分支节点中的元素个数不小于\lceil \frac{M}{2} \rceil - 1的性质。因此,在和父节点合并后,将父节点为当前节点继续向上调整,直到不违反B树的任意一条性质,调整图示如下:

然后再删除元素 Q,删除后的形状如下所示:

同理删除剩余的元素:



最后注意删除 EDCBA即可。
删除时的借位示意
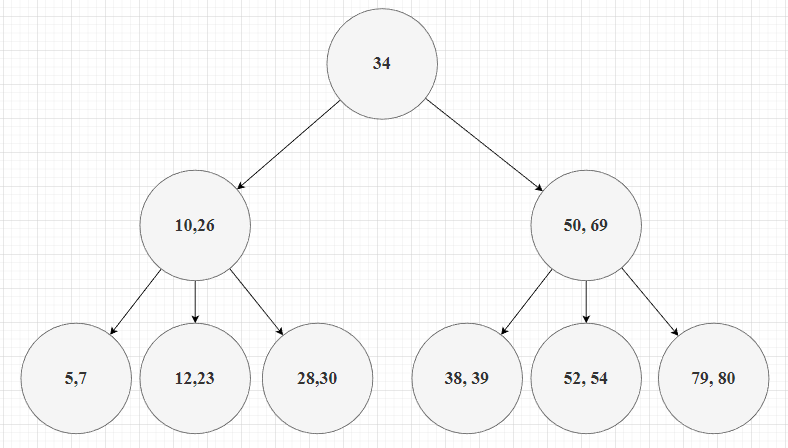
假设当前的B树为一棵5阶树,如下所示:
现删除索引值19。当查找到键值19时,发现其在叶子节点中,删除后该节点元素个数小于2,需要进行调整。发现其右孩子的元素个数大于下限值,因此可以从其右兄弟中借位元素26,即以父节点中的元素23为支点左旋,将23下沉到其左孩子,而其右孩子的最小值上升到23的位置,调整结果如下所示:
左旋也是同理,故不赘述。
删除操作实现
主逻辑
template <typename T>
void btree<T>::remove(const key_type_t& key) {
size_t index_in_finded = 0;
// 找到当前key值所在的节点,并返回其在节点中的索引值和该节点的父节点的指针
btree_node *finded_node = find(key, index_in_finded);
if (!finded_node) { // 没有找到
return;
}
// 2. 判断删除的类型
// 2.1 如果是非叶子类型,则用其后继节点中的key值覆盖这个值,且这个待删除的key值一定在叶子节点处
// 删除流程转为删除叶子节点。注:覆盖的key值一定在叶子节点的证明使用反证法即可
if (!finded_node->leaf) {
btree_node *succ = find_successor(finded_node, index_in_finded); // 不可能出现单分支的情况,所以不需要父节点指针
assert(succ != nullptr);
key_type_t &succ_key = succ->keys[0];
finded_node->keys[index_in_finded] = succ_key;
// 流程转为删除当前叶节点
finded_node = succ;
index_in_finded = 0;
}
// 2.2 如果是叶子类型,则直接进行删除后,递归调整
remove(finded_node, index_in_finded);
if (finded_node->num == 0) {
// SAFE_DELETE_NODE(finded_node);
if (!root->num) { // 留一个哨兵节点
return;
}
destroy_node(finded_node);
}
}
查找给定节点的后继节点
由于是按照键值递增的顺序存储的,则其一定是当前键值的右孩子中的最小值:
template <typename T>
typename btree<T>::btree_node*
btree<T>::find_successor(const btree_node *node, const size_t& index) const {
// 1. 如果当前节点为空,则直接返回nullptr
if (!node) {
return nullptr;
}
// 注意,在调用这个函数的时候,node一定不是叶子节点
assert(!node->leaf);
btree_node *cursor = node->children[index + 1];
while (!cursor->leaf) {
cursor = cursor->children[0];
}
return cursor;
}
删除指定节点中的元素
// 此处是叶子节点的删除
template <typename T>
void btree<T>::remove(btree_node *finded, size_t index) {
// 1. 先删除当前的这个元素
shrink_to_remove(finded, index);
// 2. 判断当前叶子节点的状态
if (finded->num >= minimum_branches - 1) {
return;
}
// 3. 循环调整
btree_node *cursor = finded;
// 如果当前节点未满足B树的性质
while (cursor->num < minimum_branches - 1) {
btree_node *parent = cursor->parent;
if (!parent) { // 此时,就剩下根节点一个节点了,此时一定满足B树性质
return;
}
// 找到当前节点位于parent节点的第几个分支
for (index = 0; index <= parent->num; ++index) {
if (parent->children[index] == cursor) {
break;
}
}
assert(index <= parent->num);
// 要么从左子树借,要么从右子树借
btree_node *left_brother = (index - 1 >= 0 ? parent->children[index - 1] : nullptr);
btree_node *right_brother = (index + 1 <= parent->num ? parent->children[index + 1] : nullptr);
// 如果能够一步调整完毕,则一步调整
if (left_brother && left_brother->num + 1 > minimum_branches) {
// 从左兄弟借,以父节点为支点,右旋
btree_right_rotate(left_brother, cursor, index);
return;
} else if (right_brother && right_brother->num + 1 > minimum_branches) {
// 从右兄弟借
btree_left_rotate(right_brother, cursor, index);
return;
}
// 量兄弟都不能借,则需要父节点合并
// 1.是跟左孩子合并?还是和右孩子合并?
if (left_brother) { // 和左兄弟合并
btree_merge_nodes(left_brother, cursor, index);
} else { // 和右兄弟合并
btree_merge_nodes(right_brother, cursor, index);
}
// 已经平衡到根节点了,无需平衡了,直接结束调整
if (!parent->num) {
// SAFE_DELETE_NODE(parent);
destroy_node(parent);
return;
}
cursor = parent;
}
}
删除叶子节点中的元素
由于在节点中是使用数组存储的,因此其实就移动元素进行覆盖操作
template <typename T>
void btree<T>::shrink_to_remove(btree_node *node, size_t index) {
for (size_t i = index + 1; i < node->num; ++i) {
node->keys[i - 1] = node->keys[i];
}
node->num--;
}
左旋操作
template <typename T>
void btree<T>::btree_left_rotate(btree_node *brother, btree_node *current, size_t index) {
btree_node *parent = current->parent;
assert(parent != nullptr);
btree_node *right_brother = brother;
// 父节点的key下去,右兄弟的第一个key值上去
key_type_t &key_in_parent = parent->keys[index];
key_type_t &key_in_brother = right_brother->keys[0];
// insert(current, key_in_parent);
append_key_with_given_node(current, key_in_parent);
key_in_parent = key_in_brother;
shrink_to_remove(right_brother, 0);
}
右旋操作
template <typename T>
void btree<T>::btree_right_rotate(btree_node *brother, btree_node *current, size_t index) {
btree_node *parent = current->parent;
assert(parent != nullptr);
btree_node *left_brother = brother;
key_type_t &key_in_parent = parent->keys[index - 1];
size_t last_elem_index = left_brother->num - 1;
key_type_t &key_in_brother = left_brother->keys[last_elem_index - 1];
// 左兄弟的最后一个key值上升到parent;parent的key值下降到其右孩子(current)节点
append_key_with_given_node(current, key_in_parent);
key_in_parent = key_in_brother;
shrink_to_remove(left_brother, last_elem_index);
}
合并操作
template <typename T>
void btree<T>::btree_merge_nodes(btree_node *brother, btree_node *current, size_t index) {
btree_node *parent = current->parent;
assert(parent != nullptr);
btree_node *left_brother = nullptr, *right_brother = nullptr;
if (index - 1 >= 0 && parent->children[index - 1] == brother) {
left_brother = brother;
} else {
right_brother = brother;
}
// 如果是左孩子,父节点,当前节点;则合并到左孩子上,然后释放掉当前节点
// 记录在父节点中的key在keys数组中的索引
size_t parent_key_index = index;
if (left_brother) {
parent_key_index = index - 1;
size_t last_child_index = left_brother->num + 1;
// 先将父节点的key值插入到左孩子的后面
// 然后将当前节点的值也合并到左孩子
// 然后拷贝children到对应的位置
append_key_with_given_node(left_brother, parent->keys[parent_key_index]);
for (int i = 0; i < current->num; ++i) {
btree_node *child = current->children[i];
if (child) {
left_brother->children[last_child_index++] = child;
current->children[i]->parent = left_brother;
}
append_key_with_given_node(left_brother, current->keys[i]);
}
btree_node *child = current->children[current->num];
if (child) {
left_brother->children[last_child_index] = child;
child->parent = left_brother;
}
// SAFE_DELETE_NODE(current);
destroy_node(current);
current = left_brother;
} else {
// 如果是当前节点,父节点,右孩子;则合并到当前节点上,然后释放掉右孩子
size_t last_child_index = current->num + 1;
// 然后拷贝children到对应的位置
// insert(current, parent->keys[parent_key_index]);
append_key_with_given_node(current, parent->keys[parent_key_index]);
for (int i = 0; i < right_brother->num; ++i) {
if (right_brother->children[i]) {
current->children[last_child_index++] = right_brother->children[i];
right_brother->children[i]->parent = current;
}
append_key_with_given_node(current, right_brother->keys[i]);
}
if (right_brother->children[right_brother->num]) {
current->children[last_child_index] = right_brother->children[right_brother->num];
right_brother->children[right_brother->num]->parent = current;
}
destroy_node(right_brother);
}
// 当合并完毕后,父节点的key值个数为0,证明是根节点,则移动树的根指针到合并后的节点并释放父节点
shrink_to_remove(parent, parent_key_index);
if (!parent->num) {
root = current;
current->parent = nullptr;
}
}
总结
- 分裂操作只发生在插入操作
- 借位和归并的操作只会发生在删除操作
B树与红黑树
红黑树其实就是一棵2-3-4树的一种实现方式,本质上和2-3-4树一致。
- 0
-
分享