高级数据结构:红黑树的拆解与实现
编辑
红黑树的定义
通俗理解,红黑树是一棵添加了额外限制的二叉排序树。它的本质还是一棵二叉排序树,只是添加了一些其他的规则,以使得它可以做到自平衡。
严格意义上来讲,满足以下5条性质的二叉排序树是一棵红黑树:
- 每个节点只有两种颜色,要么是红色的,要么是黑色的。
- 跟节点一定是黑色的,即:根节点必须是黑色的
- 每个叶子节点也是黑色的,即:叶子节点必须是黑色的
- 如果一个节点是红色的,则它的两个儿子节点一定都是黑色的
- 对每个节点,从该节点到其子孙节点的所有路径上包含的黑色节点数目是相同的
对于性质五,红黑树的作者的说法是:
Every simple path from a given node to any of its descendant leaves contains the same number of black nodes.
即:从任意给定节点出发到它自身任何后代叶子的所有简单路径,均包含相同数目的黑色节点数目。通过这个性质可以发现,红黑树是黑色节点的完美二叉平衡树,而如果包含红色节点的话,其并不是一棵完美平衡二叉树。
根据上述定义,在脑海中有一个简单的图像:
- 树根和叶子全是黑色的
- 红色节点的两个孩子也都是黑色的(局部上看)
- 从当前这棵树的根节点到叶子节点的所有路径上包含的黑色节点数是相同的(这个是宏观上看,或者说整体上看,从而这个性质决定了红黑树的平衡(高度))
注意区分:树的高度是从叶节点出发开始计算;树的深度是从根节点出发开始计算。
根据定义性质五,有一个直观的感受:红黑树中,由于最短路径上的黑色节点数目和最长路径上的黑色节点数目是相同的,那么最长路径和最短路径上的节点数目的关系是什么呢?首先,构造一个最短的路径,由于根节点要求是黑色的,叶子节点要求是黑色的。那么最短的路径上的黑色节点数目一定是2个。然后,构造一个最长的路径,其要保证只有两个黑色节点,那么它最长只能加一个红色节点,不能再加额外的节点了,所以最长路径上的节点数目是3;而如果最短路径上的黑色节点数为3的时候,最长路径中可有2个红色节点,即共有5个节点。通过数学归纳法可证它们之间的关系是:,其中,指的是路径当中所包含的黑色节点数目,是最长路径的所有节点数目。
所以上面的疑问也就解答完毕了,最大路径和最小路径之间的高度差,差值最大为:,两者之差不会过大,导致退化为链表,查找效率降低的过多
注意:红黑树不能全为黑色节点,可以使用反证法进行证明。如果一棵平衡的红黑树全是黑色的节点,新插入的节点也是黑色的,那么无论怎么做调整,这棵树都不会再平衡,因此一棵红黑树不能全为黑色节点。
左旋与右旋操作
在删除一个旧节点或者插入一个新节点后,当前的红黑树可能就不满足红黑树的性质(定义)了,那么就需要做调整。本小节就是讲解如何调整才能使其重新成为一棵红黑树中用到的局部操作——左旋和右旋。
所谓左旋,就是向左旋转;右旋,就是向右旋转。举个例子来说,对于两个节点x和y,其位置关系只有两种,一种是节点y是x的子树,则左旋就是将x变为y的子树;另一种情况是x是y的子树,则右旋就是将y变为x的子树。
左旋和右旋是一对互为逆的操作,即这两个操作均是可逆的。当你通过左旋变换完毕后,可以使用右旋变回来;当你通过右旋变换完毕后,可以使用左旋变回来。图示如下:
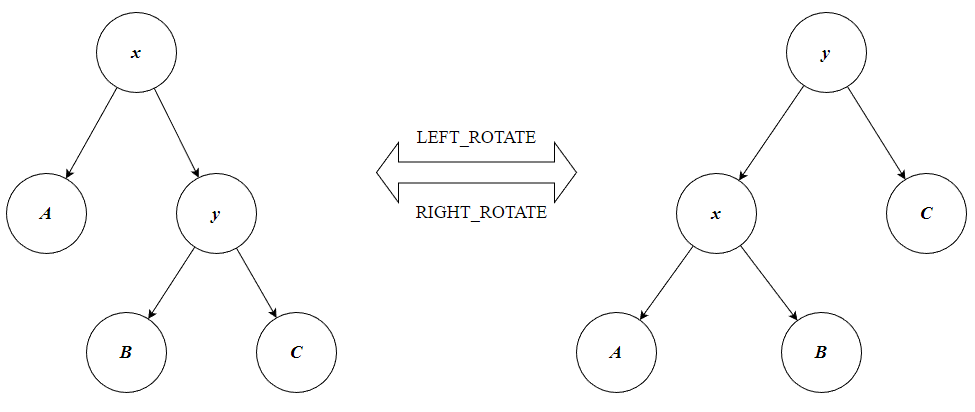
上述图示中:节点A, B 和C 不是单纯的单一节点,而是分别以它们为根节点的树。
在做左旋的时候,支点就是节点x ,而在做右旋的时候,支点就是y ,即谁转谁就是支点。对于二叉排序树来说,左旋和右旋有一个很好的性质:做完左旋或右旋后,并不会影响二叉排序树的性质。
左旋和右旋可以简记为:
- 左旋:支点变为自己右孩子的左孩子
- 右旋:支点变为自己左孩子的右孩子
左旋和右旋操作在平衡二叉树(AVL树)中的作用是在插入或删除节点之后,造成左右子树高度差超过某一阈值后,通过左旋或右旋等操作降低两棵子树之间的高度差,使两者的高度差变化到可以接受的范围内。而红黑树是一棵黑色节点的自平衡的二叉排序树,其也可以通过左旋和右旋操作,辅之以变色操作即可使得黑色节点数在插入或删除操作之后保持平衡。
红黑树的相关操作
红黑树的插入
插入平衡调整
新插入的节点的插入规则首先是通过二叉排序树的规则找到要插入的位置,而插入的节点颜色是什么?由于黑色节点会改变树的高度,所以插入的节点的颜色应该是红色的。
而新插入节点的位置,一定是比叶子节点高一层的那个,也就是插入到的是除了叶子节点那一层外的最底层,而插入的颜色一定是红色。
在插入新节点之后,可能会改变红黑树的性质,因此需要进行自底向上的调整。那么需要总结归纳一下,什么情况下,新插入的节点会打破红黑树的性质,即:都会打破红黑树的哪几条性质?只能打破第4个性质,即:如果一个节点是红色,它的左右孩子一定是黑色。但是新插入的节点是红色的,如果其父节点也是红色的话,则会导致与这条性质矛盾。
那么如何调整呢?要抓住重点,只需要将多余的红色给它干掉就可以了。在调整的过程中,在不违反红黑树其他四条性质和二叉排序树的性质的前提下,通过某些手段,让它恢复第四条性质即可。在分析的时候,要抓住不变量和改变量,穷举出所有的可能,然后归纳总结出对每一种情况都如何进行调整即可。
首先,对插入操作中出现的各个节点进行命名约定:
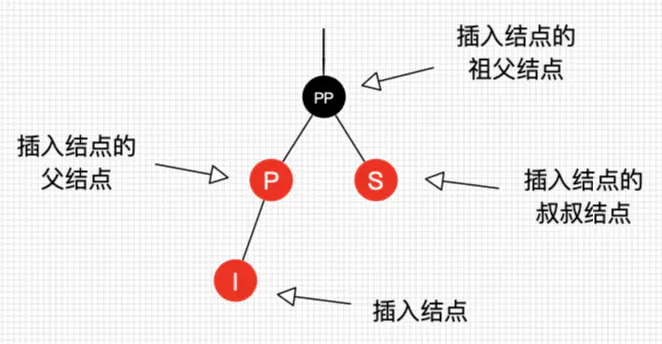
其中:
- 插入的节点为
i - 插入节点的父节点为
P - 插入节点的祖父节点为
PP - 插入节点的叔父节点为
S
然后,明确现在的目标。现在的目标是:如何做最少的动作,对插入后的某一局部做调整,以恢复整棵树的红黑树性质,也就是所谓的平衡。那么首先就需要进行确定的是,这个局部到底是多局部?换句话说,就是这个局部都包含哪些必要的节点,对这些节点进行操作,就可以使得这棵二叉排序树恢复平衡。穷举思路是逐一扩大范围,然后从小到大进行分析验证:
- 只包含插入节点
I和父节点P - 包含插入节点
I和父节点P,此外还包含叔父节点S - 包含插入节点
I和父节点P,此外还包含叔父节点S和祖父节点PP
在验证时再次强调一下现有的前提:
- 由于红黑树上的所有叶子节点均为黑色,因此将所有叶子节点隐去了,也就是说图像中绘制出来的任一节点均有左孩子和右孩子。
- 在插入节点
I之前,这棵二叉排序树一棵平衡的红黑树
再强调一下现在的目的:确定至少需要包含哪些节点,才能使得这课局部子树恢复平衡。对于前两种情况有:
- 对于情况1,由于插入的节点的颜色是红色的,其父节点也是红色的。如果只在这两点之间做操作而不引入其他节点,想要去掉多余的红色只能是其中任意一个改变颜色,而改变的颜色只能是黑色,此时会改变子树的黑高。此时情况劣化了,除了违反性质4,还违反了性质5,因此只包含节点
I和节点P是不行的。 - 对于情况2,如果想要将红色节点传递给叔父节点,就需要联系纽带, 而要使得叔父节点
S和父节点P产生联系,就必须要有祖父节点PP,否则不知道父节点和叔父节点的位置(比如说,无法知道叔父节点到底是位于祖父节点的左孩子还是右孩子),也无法直接进行平衡,因此不包含祖父节点PP也是不行的。
对于情况3来说,具体还需要进一步细分。先分离变量,使用控制变量法,先不考虑颜色,只考虑二叉树的形状,即:现在在已知插入节点I、父节点P、叔父节点S和祖父节点PP,这棵局部二叉树的形状都有哪几种可能?根据父节点的位置来划分,可以划分为两种:
- 父节点
P是祖父节点PP的左孩子 - 父节点
P是祖父节点PP的右孩子
由于上述两种情况是对称的情况,因此只需要考虑其中一种即可。假设现在的情况是父节点P是祖父节点PP的左孩子,在这个条件下,这棵局部二叉树的形状还有哪几种?答案是只有两种可能。因为有一个前提,即:所有叶子节点隐去了。具体的情况如下:
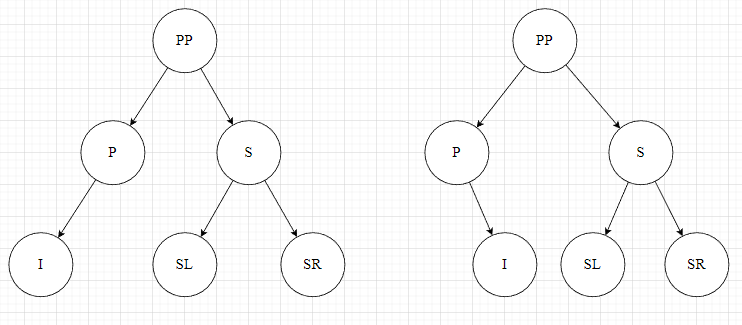
在上述图示中,隐去了叶子节点以及插入节点I的兄弟节点。因为在插入之前其就是一棵平衡的红黑树,插入节点的兄弟节点不论是否是叶子节点,都不违反红黑树的性质,因此其不影响结果,故隐去;而叔父节点的两个孩子SL和SR绘制出来是因为,其颜色可能有多种情况,不一定只是叶子节点的黑色的情况,因此其在后续染色的讨论中是需要出现的,因此并不能隐去,而是假设其存在。
现在控制局部二叉排序树的形状,变节点的颜色,看看都有哪些情况。现在假设其是上述两种形状的左侧形状,令其为形状1。在开始上色之前,确定一下现在的确定性因素有:
- 插入节点
I的颜色是红色的 - 父节点
P的颜色是红色的 - 祖父节点
PP的颜色一定是黑色的(因为父节点的颜色是红色的,且插入之前是一棵平衡的红黑树,因此PP一定不能是红色的) - 这棵局部二叉树是一棵二叉排序树
- 这棵局部二叉树中除了性质4以外的其他性质均满足
那么现在颜色上的不确定因素有:叔父节点S及其两个孩子SL和SR的颜色均未知。现在假设:
- 叔父节点
S是红色。则有:叔父节点的两个孩子节点SL和SR一定都是黑色的(根据性质3) - 叔父节点
S是黑色。则叔父节点的两个孩子节点的颜色未知,具体可分为三种情况:- 左孩子
SL和右孩子SR均是黑色的 - 左孩子
SL是红色的,右孩子SR是黑色的 - 左孩子
SL和右孩子SR均是红色的
- 左孩子
- 虽然有3种情况,但是这3种情况中的任意一样都不需要讨论。原因是在插入节点
I之前,这棵树是一棵平衡的红黑树,因此在左子树中插入一个红色节点I并不会影响到右子树的黑高。因此它是什么颜色,都不会影响后续的变化。
对于第一种情况,仅通过这些局部点的调整能恢复吗?由于祖父节点PP的颜色是黑色的且位于公共节点的位置,其以两个孩子节点P和S 为根的子树上的共享这一个黑高,因此只需要黑色节点下沉,分裂到左右两棵子树上,而红色节点上浮,就可以平衡了,即:只需要父节点P和叔父节点S的颜色变黑,祖父节点PP的颜色变红即可(颜色由黑红红翻转为红黑黑)。这个过程相当于是红色上浮的过程,因此我称之为冒泡。
对于第二种情况,其由于上面的讨论可知,叔父节点S的两个子孩子的颜色不会影响黑高,则其形状可以简化为:
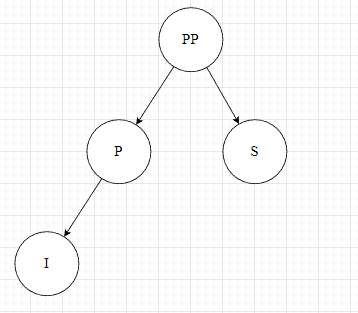
此时,颜色为:祖父节点PP和叔父节点S是黑色,插入节点I和父节点P为红色。如果像情况1直接改变颜色,会影响节点PP左右子树的黑高,违反红黑树的性质5。能否借鉴平衡二叉树的旋转操作(注意:旋转操作不会改变二叉排序树的性质),将红色冒泡出去呢?以祖父节点PP为支点进行右旋,此时节点PP下移到右子树,节点P上移到原节点PP的位置。由于公共位置的黑色节点PP下沉到了一侧,另一侧少了一个黑色节点,则只需要将节点PP和P的颜色翻转,即:祖父节点PP变为红色,父节点P变为黑色即可平衡。
当插入节点I是父节点P的右子树时,其也有两种情况,其第一种情况就是叔父节点S是红色,处理方法与上述情况1一致;而情况2则略有不同。无法直接以祖父节点PP为支点直接右旋进行调整,而是得先以父节点P为支点左旋,得到上述情况2的情形后,再右旋调整。
综上,以父节点是祖父节点的左孩子还是右孩子可分为两大类;而每一大类又有三种情况。这两类的处理方法是对称的,因此只需要掌握其中一大类中的3种情况的处理办法,就可以得到另一大类的处理办法了。
需要特别提出的是:在做插入调整的时候,是站在插入节点的父节点的位置进行调整的。这是由上面分析讨论所得出来的。上述分析讨论并归纳总结出来的情况,其实都可以以插入节点的父节点的角度进行分类,分类标准就是两种:
- 父节点位于祖父节点的左孩子的位置还是右孩子的位置,从而可以确定父节点的兄弟节点的位置
- 新插入的节点位于父节点的左孩子的位置还是右孩子的位置,从而可以确定新插入节点的兄弟节点的位置
上面两个分类标准确定后,该局部二叉排序树的形状也就确定下来了,从而按照控制变量法,分情况讨论兄弟节点的颜色,从而就可以得到上面的三种情况了。
其实插入操作平衡的核心是抓住红黑树的性质5,而在旋转前变色,则是保证在旋转过程中红黑树的性质5不变(因为违反的是性质4)。根据上述技巧,则则只需要看在旋转后,各自分支都少了什么类型的节点,缺啥补啥,就可以确定旋转前后各个节点应该变为什么颜色了。
插入平衡调整示例
下面的示例中的均是插入节点的父节点位于祖父节点的左孩子的位置的前提下进行调整的。
第一类:叔父节点的颜色是红色的。
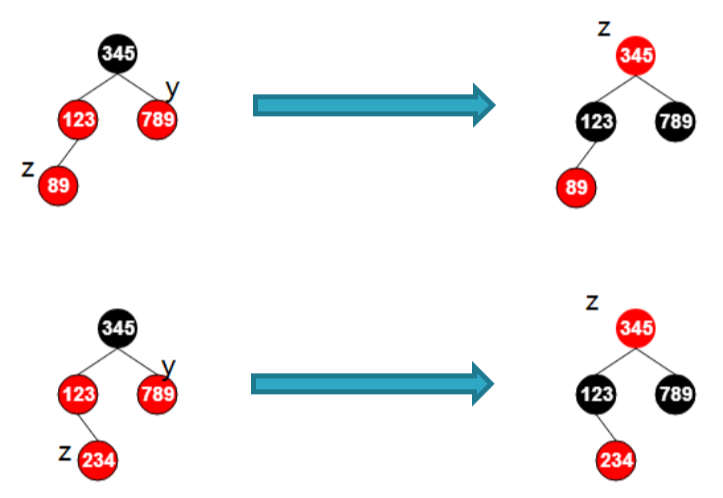
第二类:当前插入的节点是父节点的右孩子,而叔父节点的颜色是黑色的,

第三类:当前插入的节点是父节点的左孩子,而叔父节点的颜色是黑色的

插入操作的伪代码
使用文字描述的形式描述一下插入平衡的逻辑:
-
如果红黑树此时是棵空树,则把新插入的节点作为该棵树的树根,并染成黑色。
-
如果待插入节点的
key值在树中已经存在,有多种处理方法,具体处理按照项目要求(具体情况)进行设置,不限于:拒绝和更新等操作。 -
如果待插入节点的父节点为黑色,直接插入待插入节点,并将其设置为红色。
-
如果待插入节点的父节点为红色,由于违反了红黑树的第五条性质,需要进行平衡性调整。在平衡性调整的过程中,按照待插入节点的父节点位于祖父节点的左子树还是右子树分为两大类,而每大类按照其叔父节点颜色的不同又分为三种情况。由于两大类是对称的情况,因此只需要编写其中一类,另一类对称修改即可。
-
叔父节点是红色的,直接将祖父节点、父节点和叔父节点变色即可,变为红,黑,黑的形式
-
叔父节点不存在或者是黑色的(由于不存在的情况是叶子节点的情况,而叶子节点是
nil节点,包括所有红黑树的性质,所以它一定是黑色的) -
如果当前节点是父节点的左孩子,将父节点设置为黑色,祖父节点变为红色,然后对祖父节点进行右旋
- 如果当前节点是父节点的右孩子,先对父节点左旋后变为上述第一种情况,然后再进行处理
-
红黑树的删除
删除平衡的调整
删除策略大体上与二叉排序树的删除节点的策略相同,即:如果删除的是叶子节点,则直接删除该节点即可;如果删除的不是叶子结点,则找到其直接后继(即:第一个比它大的节点或者直接前驱,即:最后一个比它小的节点)与要删除的节点交换,然后删除交换后的节点即可。之所以说大体上一致,是因为红黑树的删除可能会造成不满足红黑树的性质的情况出现,此时需要调整红黑树。
在删除的时候,所面临的情况有以下三大类:
- 要删除的节点不包含左右子树,直接删除即可
- 要删除的节点只包含左子树或只包含右子树,将待删除节点的左子树或者右子树上移,改变其父节点的指向后,删除待删除节点;
- 待删除节点既包含左子树,又包含右子树的情况,此种情况最复杂,也是最一般的情况。
上面的这三种情况是对于平衡二叉排序树的删除规则,即:将待删除节点的直接后继中的值覆盖待删除节点,然后流程转为删除其直接后继节点,从而将情况转为情况1或者情况2。按照上述规则进行删除,并不会影响二叉排序树的性质。如果红黑树按照上述规则进行删除,其能够保证红黑树的二叉排序树的性质的不变,但是可能会影响红黑树的平衡(即违背了红黑树的某些性质),那么什么情况下删除一个节点会影响红黑树的性质呢?
- 当删除的节点是红色节点。由于删除该节点之前,原红黑树平衡,那么删除了红色节点后并不会影响红黑树的其他性质(不会出现两个红色节点相邻以及改变黑高等情况)。
- 但删除的节点是黑色节点。而此时就可能会出现红黑树的性质的改变,即:
- 当删除的节点不是树的唯一节点,则删除的节点是黑色节点一定会违背性质5,即影响黑高
- 当删除的节点的唯一非空子节点是红色,而被删节点的父节点也是红色,则会违背性质4
- 当删除的节点的唯一非空子节点是红色,且被删节点是树根,则会违背树根必须是黑色的性质,即性质2.
故可以得出结论,当删除的节点是黑色节点就可能造成红黑树不平衡。在删除节点造成不平衡后,如何调整呢?具体分析还是老套路,控制变量法 + 分类讨论,即:先确定当前局部二叉树的形状后,再加上颜色的变化。再次强调此时讨论的前提:在删除一个节点之前,这棵树是一棵平衡的红黑树,其满足红黑树的所有性质。这里讨论一般情况,即:删除的节点有两个孩子节点,且其颜色为黑色。根据被删除的节点位于根节点的左子树还是右子树,可以分为两种情况,因为是对称的,因此只需要讨论其中的一种情况。现假设被删除的节点位于根节点的左侧,删除节点z 则有两种情况:
- 删除后的第一种情况:替代节点
y的唯一非空子孩子位于删除后的节点的父节点的左孩子
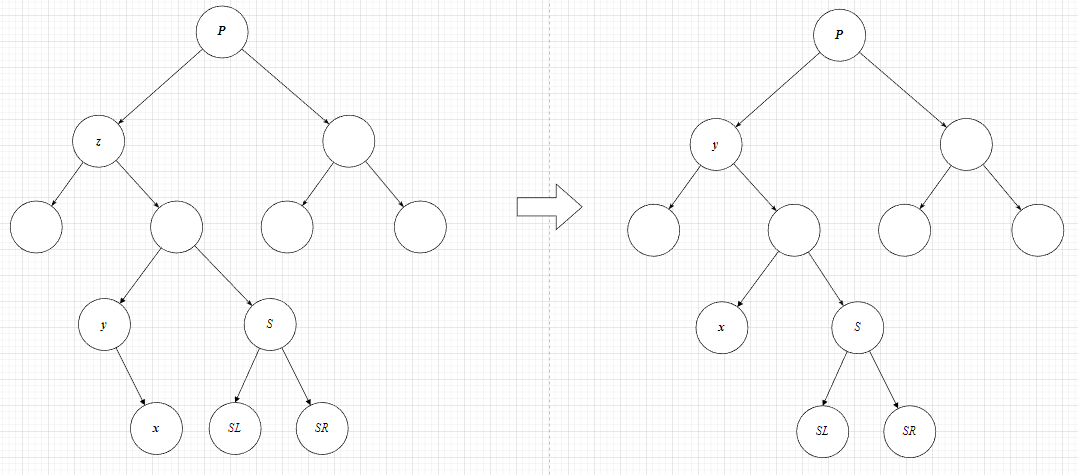
- 删除后的第二种情况:替代节点
y的唯一非空子孩子位于删除后的父节点的右孩子

这两种形状也是对称的,因此只需要讨论一种即可,本文后面的讨论是基于删除后的情况1进行套路的,即:替代节点y 的唯一非空子节点x位于删除节点后的父节点的左侧,即:x 是左孩子的情况。
在形状确定后,就要控制颜色了,而由于形状和颜色不同造成的违反的红黑树的性质的不同,从而造成情况复杂,红黑树的作者提出了一个小技巧:
我们从被删结点后来顶替它的那个结点开始调整,并认为它有额外的一重黑色。这里额外一重黑色是什么意思呢,我们不是把红黑树的结点加上除红与黑的另一种颜色,这里只是一种假设,我们认为我们当前指向它,因此空有额外一种黑色,可以认为它的黑色是从它的父结点被删除后继承给它的,它现在可以容纳两种颜色,如果它原来是红色,那么现在是红+黑,如果原来是黑色,那么它现在的颜色是黑+黑。有了这重额外的黑色,原红黑树性质5就能保持不变。现在只要恢复其它性质就可以了,做法还是尽量向根移动和穷举所有可能性。
使用上述技巧的话,需要注意2个重要前提:
- 在删除该黑色节点前,原红黑树是有一棵平衡的红黑树
- 在删除该黑色节点之后,其唯一子孩子继承了被删除节点的黑色,从而并不会违反性质5。排除了一种可能,只需要恢复其他可能违反的性质即可(如性质2和性质4)
而我们的目标是:将双黑节点往上冒泡,直到根节点。在此过程中,如果已经能够消除多余的一重黑(即红+黑 = 黑),此时停止调整,不用等到冒泡的根节点后,将根节点修改为单黑才结束。
先根据被删除节点的唯一非空子孩子的颜色不同进行分类:
- 当非空子孩子是红色的时候,红色 + 黑色 = 黑色。不论在节点删除后,非空子孩子的父节点是什么颜色,都不会影响红黑树的其他性质,因此红黑树自动平衡。
- 当非空子孩子是黑色的时候,黑色 + 黑色 = 双黑。此时不满足红黑树的性质1,即:红黑树的节点只有两种颜色,要么是黑色,要么是红色。此时需要调整。
对于第二种情况,即:**被删除节点的唯一非空子孩子的颜色是双黑(即拥有额外一重黑标记)**的情况。改变其颜色,共有:
- 双黑节点的兄弟节点是黑色的
- 双黑节点的兄弟节点是红色的
两种情况。而至少需要哪些节点才能进行平衡呢?,需要:
- 双黑节点
x - 双黑节点的父节点
P - 双黑节点的兄弟节点
S - 兄弟节点的两个子孩子
SL和SR
具体为什么需要这么几个节点的原因与插入平衡的情况类似,这里不展开了。
双黑节点的兄弟节点是黑色
由于兄弟节点是黑色,其父节点P 和两个子孩子SL和SR的颜色是不确定的,因此需要分类讨论:
- 兄弟节点的两个子孩子均是黑色
- 兄弟节点的左孩子是红色,右孩子是黑色
- 兄弟节点的左孩子是黑色,右孩子是红色
- 兄弟节点的左孩子是红色,右孩子是红色
而再加上父节点的两种颜色,一共是8种情况。
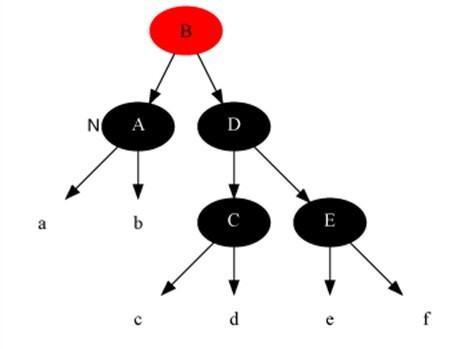
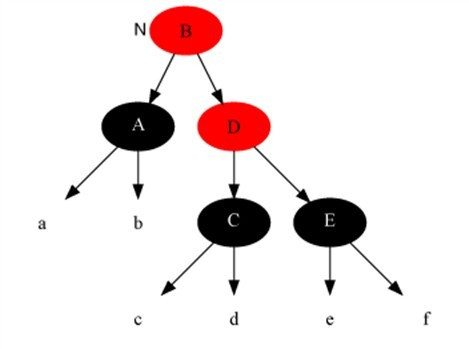
当兄弟节点的两个子孩子均是黑色的情况,此时可以将兄弟节点和当前双黑节点提取公因子,抽出一重黑出来(即:兄弟节点变为红色,当前标记的双黑节点取消标记变为单黑节点),给到其父节点,使得父节点变为新的双黑节点,此时当前节点转为父节点,双黑节点上浮完毕。此时,由于父节点的颜色是不确定的,可能是黑色,也可能是红色,因此标记完父节点具有额外一重黑色之后,应以父节点为当前节点,进入下一次调整。如果父节点是红色,则在下一轮调整直接退出,并将父节点红 + 黑 = 黑色(因为此时是朴素情况);如果父节点是黑色,则如果其不是根节点,则继续进行调整(在分类讨论的时候别忘记目标:除非能直接将双黑节点直接消除,否则一直冒泡到根节点),图示如下(注意图里面的根节点B的颜色是任意画的,因为可以是黑色也可以是红色):
情况2:双黑节点的兄弟节点的左孩子是红色,右孩子是黑色的情况。此时不能直接提取公因子,将双黑节点和兄弟接地各自上浮一重黑色给父节点,因为兄弟节点中的子节点有一个是红色的,兄弟节点黑色上浮后,会违反性质4。那么目标就是想办法对该局部进行变换,以可以最终提取公因子。可以以兄弟节点为支点右旋,将红色节点上浮。而此时公共黑节点下沉到右子树上了,使得违反性质5了。因此在旋转前,将兄弟节点变成红色,其左孩子变成黑色。此时,性质5仍然满足,而情况仍然是双黑节点的兄弟节点是黑色的情况。图示如下图:
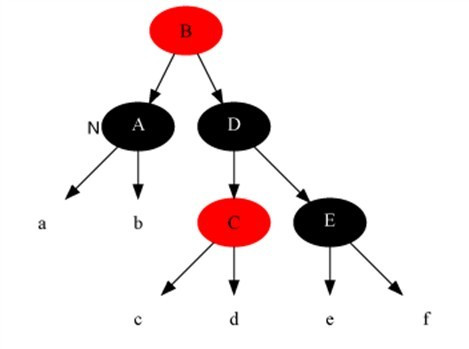
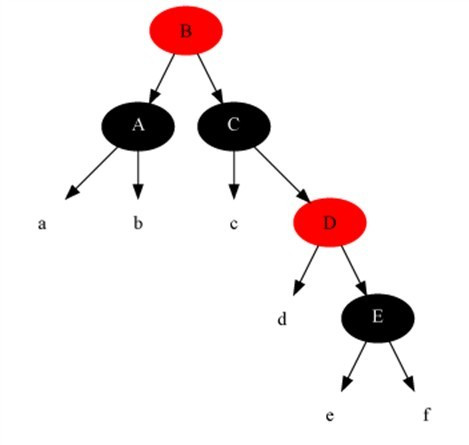
情况3和情况4其实是一种情况,也是情况2最终转变成的情况,即:**双黑节点的兄弟节点的左孩子颜色任意,右孩子是红色的情况。**此时的情况同情况2,由于兄弟节点至少有一个子孩子是红色的,不能各自直接上浮一重黑。可以将双黑节点和兄弟节点的父节点为支点进行左旋,从而将兄弟节点上浮,此时不会违反二叉排序树的性质,也不会违反红黑树的性质四。旋转前的不确定因素有:
- 父节点的颜色是不确定的
- 兄弟节点的左孩子的颜色是不确定的
共4种情况,那么依次对这4种情况进行讨论。
情况1:当父节点是红色的,兄弟节点的左孩子是红色的。旋转后,选择前后的父节点的颜色冲突(两个红色了),因此需要其中一个修改为黑色;而兄弟节点上浮为根节点,成为公共节点,路径上的黑色节点数目也改变了,同时违反了两种性质。那么能平衡掉吗?只需要在旋转前:
- 将父节点修改为黑色(相当于左旋后,双黑节点上浮了一重黑,红+黑为黑色)
- 兄弟节点改为红色
- 兄弟节点的右孩子变为黑色
此时上述违反的性质,在旋转后就可以得到恢复。而此刻双黑节点消除完毕,整棵树恢复了红黑树的性质。退出调整
情况2:当父节点是红色的,兄弟节点的左孩子是黑色的。由于黑色的兄弟节点上浮为根节点,成为公共节点,违反了性质5,因此在旋转前:
- 将父节点变为黑色(相当于左旋后,双黑节点上浮了一重黑,红 + 黑为黑色)
- 兄弟节点改为红色
- 由于将兄弟节点改为红色,右侧分支上少了一个黑色节点,因此将兄弟节点的右孩子变为黑色。
此时上述违反的性质,在旋转后就可以得到恢复。而此刻双黑节点消除完毕,整棵树恢复了红黑树的性质。退出调整
情况3:当父节点是黑色的,兄弟节点的左孩子是红色的。在旋转后,左侧分支多了一个黑色节点,违反了性质5,因此在旋转前
- 将父节点变为红色
- 兄弟节点的右孩子变为黑色
旋转后,将双黑节点上浮到红色的节点,即:兄弟节点处。性质5得到了满足。整棵树恢复了红黑树的性质。退出调整
情况4:当父节点是黑色的,兄弟节点的左孩子是黑色的。在旋转后,左侧分支多了一个黑色节点,违反了性质5,因此在旋转前:
- 将父节点变为红色
- 将兄弟节点的右孩子变为黑色
旋转后,将双黑节点上浮到红色的节点,即:兄弟节点处。性质5得到了满足。整棵树恢复了红黑树的性质。退出调整
上述四种情况的图示如下:

上述四种情况的左侧的额外一重黑的标记为什么莫名其妙的消失了?原因是:引入额外标记是因为当前分支由于删除了一个黑色的节点(类似于小学竖式减法中的借位操作),导致黑色节点数少了一个,而通过以父节点P为支点进行左旋,并通过变色操作稳定的为缺少一个黑色节点的分支补充一个黑色节点,而其他分支并没有发生黑色节点的变化,因此此时的整棵红黑树是平衡的,可以退出平衡性调整了。
所以上述4中情况的调整策略可以统一为:
- 将兄弟节点染成父节点的颜色
- 父节点的颜色变为黑色
- 兄弟节点的右孩子变为黑色
- 以父节点为支点左旋
- 将双黑节点上浮至新的根节点,新的根节点变为当前新的双黑节点
在上面讨论的时候,情况3和情况4有一个前提,就是在调整前,其性质5是满足的,也就是兄弟节点的左右孩子节点不是直接接叶子节点的,下面是一棵棵子树,以保证路径上的黑色节点数目是相同的。
双黑节点的兄弟节点是红色
不能直接上浮黑色,因为会在公共路径上多一个黑色节点,从而违反了性质5,因此需要转换。以父节点为支点,左旋后,将情况变为双黑节点的兄弟节点是黑色的。由于左旋后,其父节点变为红色,公共节点上少了一个黑色节点,而左子树多了一个黑色节点,此时为了不违反性质5,在旋转前,需要将其父节点变红,兄弟节点变黑。这么操作的目的是将情况转为:双黑节点的兄弟节点是黑色的情况。变化示意图如下:
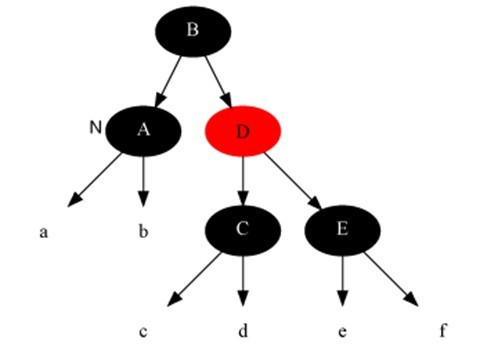

寻找给定节点的直接后继
由于红黑树是一棵二叉排序树,其直接后继指的是其中序遍历的直接后继。使用迭代法找给定节点的直接后继,只需要其满足以下条件即可:
- 如果当前节点没有右子树,则其直接后继应该是其祖先节点中左子树包含当前节点的第一个节点。描述成伪代码就是:
while (current != nullptr && current == current->parent->right_child) {
current = current->parent;
}
- 如果当前节点有右子树,则其直接后期就是其右子树中最小的那个节点,即:右子树中的最左的那个节点,伪代码为:
current = node->right_child;
while (current->left_child) {
current = current->left_child;
}
红黑树的查找
红黑树的查找同二叉排序树的查找方案。
红黑树的遍历
递归版本
中序遍历的递归版本同二叉树的中序遍历。
迭代版本
定义一个迭代器或两个函数即可。第一个函数可以命名为rbtree_first_node ,用来找树中的第一个节点;第二个函数命名为rbtree_next_node(node),用来找给定节点的直接后继。可以利用上的那个查找后继节点的方案来进行查找后继,而红黑树的第一个节点为当前树中最小的那个节点,可以描述为:
- 如果当前树为空,则直接返回
nullptr - 如果当前树的左子树不空,则第一个节点为其左子树中第一个为空的:
while (current->left_child) {
current = current->left_child;
}
红黑树的销毁
利用红黑树的查找方法和红黑树的遍历,即可直接实现销毁函数。
红黑树的实现
红黑树的节点定义
#define RBTREE_ENTRY(type) \
struct { \
struct type* left_child; \
struct type* right_child; \
struct type* parent; \
enum _rbtree_node_color color; \
}
struct _rbtree_node {
key_type_t key;
value_type_t value;
RBTREE_ENTRY(_rbtree_node) entry;
};
红黑树的整体模板类定义
template <typename Tk, typename Ty>
class RBTree {
public:
enum _rbtree_node_color {
RED = 0,
BLACK
};
private: // 数据格式定义区
#define RBTREE_ENTRY(type) \
struct { \
struct type* left_child; \
struct type* right_child; \
struct type* parent; \
enum _rbtree_node_color color; \
}
#define SAFE_DELETE_RBTREE_NODE(p) { if (p) { delete p; p = nullptr; }}
using key_type_t = Tk;
using value_type_t = Ty;
struct _rbtree_node {
key_type_t key;
value_type_t value;
RBTREE_ENTRY(_rbtree_node) entry;
};
using rbtree_node = struct _rbtree_node;
public:
// TODO: 按理说,构造函数不应该去执行可能会产生异常的操作,如何解决?
explicit RBTree() {
nil = new rbtree_node;
memset(nil, 0, sizeof(rbtree_node));
nil->entry.left_child = nil;
nil->entry.right_child = nil;
nil->entry.parent = nil;
nil->entry.color = _rbtree_node_color::BLACK;
root = nil;
}
virtual ~RBTree() {
destroy_rbtree();
}
public:
// 向红黑树中插入数据
void insert(key_type_t key, value_type_t value);
void remove(key_type_t key);
void traversal(const std::function<void(key_type_t, value_type_t)>&);
private:
void traversal_recursion(const std::function<void(key_type_t, value_type_t)>&, const rbtree_node *cursor) const;
void traversal_iteration(const std::function<void(key_type_t, value_type_t)>&) const;
rbtree_node* rbtree_first_node() const;
rbtree_node* rbtree_next_node(const rbtree_node *current) const;
// 注意:旋转不改变二叉排序树的性质
// 左旋,参数为旋转支点
void left_rotate(struct _rbtree_node* x);
// 右旋,参数为旋转支点
void right_rotate(struct _rbtree_node* y);
void insert(rbtree_node *new_node);
rbtree_node* find_insertion_postion(const key_type_t& key) const;
// 从新插入的节点开始,自底向上进行平衡性调整
void insert_fixup(rbtree_node *current);
void remove(rbtree_node *node);
rbtree_node* find_remove_position(const key_type_t &key) const;
rbtree_node* find_successor(const rbtree_node *node);
rbtree_node* find_right_subtree_minimum_node(const rbtree_node *rhs_root) const;
void remove_fixup(rbtree_node *current);
void destroy_rbtree();
private:
// TODO: 由于有指针存在,所以要写:拷贝构造;移动构造;拷贝赋值运算符;移动赋值运算符重载和析构函数,一共5个,后续补齐
// TODO: 后续改写可以使用智能指针进行改写
struct _rbtree_node *root;
struct _rbtree_node *nil; // 红黑树中的空节点
};
左旋操作与右旋操作的实现
left_rotate
template <typename T, typename Ty>
void RBTree<T, Ty>::left_rotate(rbtree_node *pivot) {
rbtree_node *rhs_node = pivot->entry.right_child;
// 1. 孩子指针交换
pivot->entry.right_child = rhs_node->entry.left_child;
if (rhs_node->entry.left_child != nil) {
rbtree_node *rhs_left_child = rhs_node->entry.left_child;
rhs_left_child->entry.parent = pivot;
}
// 2. 父指针交换
rbtree_node *pivot_parent = pivot->entry.parent;
rhs_node->entry.parent = pivot_parent;
if (pivot_parent == nil) {
root = rhs_node; // 根节点
} else if (pivot_parent->entry.left_child == pivot) {
pivot_parent->entry.left_child = rhs_node;
} else {
pivot_parent->entry.right_child = rhs_node;
}
// 3. 开始旋转
rhs_node->entry.left_child = pivot;
pivot->entry.parent = rhs_node;
}
right_rotate
template <typename T, typename Ty>
void RBTree<T, Ty>::right_rotate(rbtree_node *pivot) {
rbtree_node *lhs_node = pivot->entry.left_child;
// 1.
rbtree_node *pivot_parent = pivot->entry.parent;
lhs_node->entry.parent = pivot_parent;
if (pivot_parent == nil) {
root = lhs_node;
} else if (pivot_parent->entry.left_child == pivot) {
pivot_parent->entry.left_child = lhs_node;
} else {
pivot_parent->entry.right_child = lhs_node;
}
// 2.
pivot->entry.left_child = lhs_node->entry.right_child;
if (lhs_node->entry.right_child != nil) {
rbtree_node *lhs_right_child = lhs_node->entry.right_child;
lhs_right_child->entry.parent = pivot;
}
// 3. 旋转
lhs_node->entry.right_child = pivot;
pivot->entry.parent = lhs_node;
}
红黑树的插入实现
查找插入位置
template <typename T, typename Ty>
typename RBTree<T, Ty>::rbtree_node*
RBTree<T, Ty>::find_insertion_postion(const key_type_t& key) const {
rbtree_node *cursor = root;
rbtree_node *prior = nil;
while (cursor != nil) {
prior = cursor;
if (key < cursor->key) {
cursor = cursor->entry.left_child;
} else if (key > cursor->key) {
cursor = cursor->entry.right_child;
} else {
return nullptr;
}
}
// cursor must be nil
return prior;
}
插入调整
template <typename T, typename Ty>
void RBTree<T, Ty>::insert_fixup(rbtree_node *current) {
// 当当前节点的父节点是红色的时候,需要进行调整,因为破坏了性质4
while (current->entry.parent->entry.color == _rbtree_node_color::RED) {
// 如果当前节点的父节点是祖父节点的左子树
rbtree_node *grandfather = current->entry.parent->entry.parent;
rbtree_node *parent = current->entry.parent;
if (parent == grandfather->entry.left_child) {
rbtree_node *uncle = grandfather->entry.right_child;
// 情况1:当前节点的叔父节点是红色的
if (uncle->entry.color == _rbtree_node_color::RED) {
// 当前节点、父节点和叔父节点均为红色的,祖父节点和叔父节点的两个孩子节点均为黑色的
// 此时,不论当前节点是父节点的左孩子还是父节点的右孩子,都不会影响调整策略,即:
// 由于公共路径上均有一个黑色的节点,只需要将红色节点隔离开即可,因此只需祖父节点变红
// 父节点和叔父节点变为黑色(相当于公共黑色节点变色后,向各个子分支分裂下沉)即可局部平衡
grandfather->entry.color = _rbtree_node_color::RED;
uncle->entry.color = _rbtree_node_color::BLACK;
parent->entry.color = _rbtree_node_color::BLACK;
// 由于祖父节点变成了红色,因此需要更新当前可能发生冲突的节点为祖父节点
current = grandfather;
} else { // 此时的大分类情况为:当前节点的叔父节点是黑色的
// 由于叔父节点是黑色的,而插入的节点是红色的,父节点是红色的,祖父节点的颜色不确定;
// 叔父节点的颜色是黑色的,叔父节点的两个子节点的颜色不确定,又划分为两种情况:
// 由上述确定的因素可知:不能像情况1一样直接变色平衡,因为会直接影响黑高,那么能否
// 像二叉平衡树一样,通过旋转变换,将情况转为情况1的情形
if (current == parent->entry.right_child) {
// 先通过小左旋,变为情况3
// 由于要进行旋转,current和parent均修改了,因此需要做更新
current = parent;
left_rotate(parent);
parent = current->entry.parent;
} // 情况2:叔父节点是黑色的,当前节点是父节点的右孩子,转变为情况3进行处理
// 情况3:叔父节点是黑色的,当前节点是父节点的左孩子
// 平衡方法为:父节点变黑,祖父节点变红
parent->entry.color = _rbtree_node_color::BLACK;
grandfather->entry.color = _rbtree_node_color::RED;
right_rotate(grandfather);
}
continue;
}
// 此时和上面的情况是对称的,只需要left改为right,right改为left即可
rbtree_node *uncle = grandfather->entry.left_child;
if (uncle->entry.color == _rbtree_node_color::RED) {
grandfather->entry.color = _rbtree_node_color::RED;
uncle->entry.color = _rbtree_node_color::BLACK;
parent->entry.color = _rbtree_node_color::BLACK;
current = grandfather;
} else {
if (current == parent->entry.left_child) {
current = parent;
right_rotate(parent);
parent = current->entry.parent;
}
parent->entry.color = _rbtree_node_color::BLACK;
grandfather->entry.color = _rbtree_node_color::RED;
left_rotate(grandfather);
}
}
// 最后如果调整到了根,相当于把红色冒泡到了根,根据红黑树的性质,根必须为黑色节点,因此需要涂黑
root->entry.color = _rbtree_node_color::BLACK;
}
插入
template <typename T, typename Ty>
void RBTree<T, Ty>::insert(rbtree_node *new_node) {
// 1. 根据key,找到插入的位置
key_type_t key = new_node->key;
rbtree_node *parent = find_insertion_postion(key);
if (!parent) // 此时代表树中该key值已存在,本例拒绝其插入
return;
// 2. 然后进行插入
new_node->entry.parent = parent;
if (parent == nil) { // 证明此时是空树,直接插入红色节点不会影响红黑树的性质,但是需要将其重新置为黑色
// 直接插入
root = new_node;
} else if (key < parent->key) { // 3. 此时不是空树,插入后可能会引起不平衡,需要进行调整
parent->entry.left_child = new_node;
} else {
parent->entry.right_child = new_node;
}
insert_fixup(new_node);
}
红黑树的删除实现
查找删除位置
template <typename T, typename Ty>
typename RBTree<T, Ty>::rbtree_node*
RBTree<T, Ty>::find_remove_position(const key_type_t &key) const {
rbtree_node *cursor = root;
while (cursor != nil) {
if (key < cursor->key) {
cursor = cursor->entry.left_child;
} else if (key > cursor->key) {
cursor = cursor->entry.right_child;
} else {
return cursor;
}
}
return nil;
}
查找给定节点的后继
template <typename T, typename Ty>
typename RBTree<T, Ty>::rbtree_node*
RBTree<T, Ty>::find_right_subtree_minimum_node(const rbtree_node *rhs_root) const {
// rhs_root是要找的右子树的根节点
const rbtree_node *cursor = rhs_root;
while (cursor->entry.left_child != nil) {
cursor = cursor->entry.left_child;
}
return const_cast<rbtree_node*>(cursor);
}
template <typename T, typename Ty>
typename RBTree<T, Ty>::rbtree_node*
RBTree<T, Ty>::find_successor(const rbtree_node *node) {
if (node->entry.right_child != nil) {
rbtree_node *result = nullptr;
result = find_right_subtree_minimum_node(node->entry.right_child);
return result;
}
const rbtree_node *cursor = node;
const rbtree_node *cursor_parent = cursor->entry.parent;
// 如果当前的游标节点是其父节点的右孩子,则需要继续向上查找,直到查找到当前游标节点是其父节点的左孩子为止
// 此时,游标节点的父节点就是它的直接后继
while (cursor_parent != nil && cursor == cursor_parent->entry.right_child) {
cursor = cursor_parent;
cursor_parent = cursor->entry.parent;
}
// 两种可能:nil或者非nil。而调用它的位置,不会出现nil的情况
return const_cast<rbtree_node*>(cursor_parent);
}
删除调整
template <typename T, typename Ty>
void RBTree<T, Ty>::remove_fixup(rbtree_node *current) {
// 当前节点指的是当前具有额外一重黑标记的节点
while (current != root && current->entry.color == _rbtree_node_color::BLACK) {
rbtree_node *parent = current->entry.parent;
if (current == parent->entry.left_child) {
// 情况1.如果当前节点的兄弟节点是红色的
rbtree_node *brother = parent->entry.right_child;
if (brother->entry.color == _rbtree_node_color::RED) {
// 此时需要将其转为双黑节点的兄弟节点为黑色节点的情况
// 当前父节点的颜色和兄弟节点的两个孩子节点一定是黑色的
parent->entry.color = _rbtree_node_color::RED;
brother->entry.color = _rbtree_node_color::BLACK;
left_rotate(parent);
// 左旋后,当前节点的父节点和兄弟节点改变了,因此需要更新
parent = current->entry.parent;
brother = parent->entry.right_child;
}
// 情况2:如果双黑节点的兄弟节点是黑色,且其两个孩子也都为黑色
if (brother->entry.left_child->entry.color == _rbtree_node_color::BLACK \
&& brother->entry.right_child->entry.color == _rbtree_node_color::BLACK) {
// 提取公因子,上移额外一重标记,然后重新开始循环调整
brother->entry.color = _rbtree_node_color::RED;
current = parent;
} else {
// 情况3:如果双黑节点的兄弟节点是黑色,而兄弟节点的左孩子是红色,右孩子是黑色
if (brother->entry.right_child->entry.color == _rbtree_node_color::BLACK) {
// 以兄弟节点为支点,进行右旋,变为情况4
brother->entry.left_child->entry.color = _rbtree_node_color::BLACK;
brother->entry.color = _rbtree_node_color::RED;
right_rotate(brother);
// 而旋转完后,双黑节点的兄弟节点变了
brother = parent->entry.right_child;
}
// 情况4:如果双黑节点的兄弟节点是黑色,而兄弟节点的右孩子是红色
// 调整方法为:兄弟节点和父节点的颜色一致;父节点变黑色;兄弟节点的右孩子变为黑色
brother->entry.color = parent->entry.color;
parent->entry.color = _rbtree_node_color::BLACK;
brother->entry.right_child->entry.color = _rbtree_node_color::BLACK;
// 以父节点为支点进行左旋
left_rotate(parent);
// 此时已恢复了整棵树,因此可以退出循环了
// 注意,不要用break;因为在上面退出循环的时候可能是红 + 黑的情况
// 退出时也可能是黑色标记冒泡到了根节点上,因此在本循环下面的那个覆盖black的语句是多个
// 分支的合并,因此不能单纯的break
current = root;
}
continue;
}
// 此时是双黑节点位于当前父节点的右孩子,是上面情况的对称情况,只需要镜面修改即可,
// 即:left换right,right换left
// 情况1.如果当前节点的兄弟节点是红色的
rbtree_node *brother = parent->entry.left_child;
if (brother->entry.color == _rbtree_node_color::RED) {
// 此时需要将其转为双黑节点的兄弟节点为黑色节点的情况
// 当前父节点的颜色和兄弟节点的两个孩子节点一定是黑色的
parent->entry.color = _rbtree_node_color::RED;
brother->entry.color = _rbtree_node_color::BLACK;
right_rotate(parent);
// 左旋后,当前节点的父节点和兄弟节点改变了,因此需要更新
parent = current->entry.parent;
brother = parent->entry.left_child;
}
// 情况2:如果双黑节点的兄弟节点是黑色,且其两个孩子也都为黑色
if (brother->entry.left_child->entry.color == _rbtree_node_color::BLACK \
&& brother->entry.right_child->entry.color == _rbtree_node_color::BLACK) {
// 提取公因子,上移额外一重标记,然后重新开始循环调整
brother->entry.color = _rbtree_node_color::RED;
current = parent;
} else {
// 情况3:如果双黑节点的兄弟节点是黑色,而兄弟节点的左孩子是红色,右孩子是黑色
if (brother->entry.left_child->entry.color == _rbtree_node_color::BLACK) {
// 以兄弟节点为支点,进行右旋,变为情况4
brother->entry.right_child->entry.color = _rbtree_node_color::BLACK;
brother->entry.color = _rbtree_node_color::RED;
left_rotate(brother);
// 而旋转完后,双黑节点的兄弟节点变了
brother = parent->entry.left_child;
}
brother->entry.color = parent->entry.color;
parent->entry.color = _rbtree_node_color::BLACK;
brother->entry.left_child->entry.color = _rbtree_node_color::BLACK;
right_rotate(parent);
current = root;
}
}
// 当双黑节点冒泡到根节点时,只需要一步就能恢复
current->entry.color = _rbtree_node_color::BLACK;
}
红黑树的遍历的实现
rbtree_first_node
template <typename T, typename Ty>
typename RBTree<T, Ty>::rbtree_node*
RBTree<T, Ty>::rbtree_first_node() const {
rbtree_node *cursor = root;
if (cursor == nil) {
return cursor;
}
// 如果当前树的左子树不空,则其第一个节点为左子树中的最小节点
while (cursor->entry.left_child != nil) {
cursor = cursor->entry.left_child;
}
return cursor;
}
rbtree_next_node
template <typename T, typename Ty>
typename RBTree<T, Ty>::rbtree_node*
RBTree<T, Ty>::rbtree_next_node(const rbtree_node *current) const {
// 其实就是找当前节点的后继节点
if (current->entry.right_child != nil) {
return find_right_subtree_minimum_node(current->entry.right_child);
}
// 如果当前节点不存在右孩子,则如果当前节点
rbtree_node *current_parent = current->entry.parent;
while (current != root && current == current_parent->entry.right_child) {
current = current_parent;
current_parent = current->entry.parent;
}
return current_parent;
}
traversal
template <typename T, typename Ty>
void RBTree<T, Ty>::traversal_iteration(const std::function<void(key_type_t, value_type_t)>& user_callback) const {
for (rbtree_node *cursor = rbtree_first_node(); cursor != nil; cursor = rbtree_next_node(cursor)) {
user_callback(cursor->key, cursor->value);
}
}
销毁红黑树
#define SAFE_DELETE_RBTREE_NODE(p) { if (p) { delete p; p = nullptr; }}
template <typename T, typename Ty>
void RBTree<T, Ty>::destroy_rbtree() {
rbtree_node *cursor = rbtree_first_node();
while (cursor != nil) {
rbtree_node *next = rbtree_next_node(cursor);
remove(cursor);
cursor = next;
}
// 此时是叶子节点了
SAFE_DELETE_RBTREE_NODE(cursor);
root = nullptr;
nil = nullptr;
}
- 0
-
分享